- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:21.
- Ostatnio zmodyfikowany 2025-01-23 12:43.
Podział można przeprowadzić na różne sposoby. Możesz dzielić ułamki dziesiętne, ułamki zwykłe, a nawet wykładniki i używać dzielenia długiego lub krótkiego. Jeśli chcesz poznać różne sposoby dzielenia liczb, wykonaj poniższe czynności.
Krok
Metoda 1 z 5: Wykonywanie dzielenia długich serii

Krok 1. Zapisz pytania
Aby wykonać dzielenie długie, umieść mianownik (liczbę, która będzie dzielić) poza paskiem dzielnika, a licznik (liczbę do podziału) wewnątrz paska dzielnika.
Na przykład: 136÷3

Krok 2. Podziel pierwszą cyfrę licznika przez mianownik (jeśli to możliwe)
W tym przykładzie 1 nie jest podzielne przez 3, więc umieść 0 nad paskiem dzielnika i przejdź do następnego kroku. Odejmij 1 od 0 i umieść wynik pod liczbą 1.

Krok 3. Podziel liczbę pozostałej części pierwszej cyfry licznika i drugiej cyfry licznika przez mianownik
Ponieważ 1 nie można podzielić przez 3, liczba 1 jest nadal używana. Musisz odjąć 3. Teraz podziel 13 przez 3. Ponieważ 3 x 4 = 12, umieść 4 nad dzielnikiem (na prawo od 0), następnie odejmij 13 przez 12 i zapisz wynik poniżej.

Krok 4. Podziel pozostałe liczby według mianownika
Obniż liczbę 6 na prawo od 1, aby uzyskać 16. Teraz podziel 16 przez 3. Ponieważ 3 x 5 = 15, napisz liczbę 5 na prawo od liczby 4, odejmij 16 przez 15 i zapisz wynik (16-15= 1) poniżej.

Krok 5. Napisz resztę obok ilorazu
Twoja ostateczna odpowiedź to 45 z 1 pozostałym lub 45 R1.
Metoda 2 z 5: Wykonywanie krótkich dzieleń

Krok 1. Zapisz pytania
Wpisz mianownik (liczbę do podzielenia) poza paskiem dzielnika, a licznik (liczbę do podzielenia) wewnątrz paska dzielnika. Zwróć uwagę, że przy dzieleniu krótkim mianownik nie może być dłuższy niż jedna cyfra.
Na przykład 518 4

Krok 2. Podziel pierwszą cyfrę licznika przez mianownik
5 4 = 1 R1. Umieścić iloraz (1) nad długą listwą rozdzielającą. Napisz resztę powyżej pierwszej cyfry licznika. Umieść małą 1 nad 5, aby przypomnieć, że pozostało Ci 1 po dzieleniu 5 przez 4. Liczba 518 powinna teraz wyglądać tak: 5118

Krok 3. Podziel liczbę utworzoną z reszty i drugą cyfrę licznika przez mianownik
Kolejna liczba to 11, którą otrzymuje się z wartości rezydualnej (1) i drugiej cyfry licznika (1). 11 4 = 2 R 3 ponieważ 4 x 2 = 8 z resztą 3. Wpisz wartość reszty powyżej drugiej cyfry licznika. Umieść 3 nad 1. Początkowy licznik (518) wygląda teraz tak: 51138

Krok 4. Podziel pozostałe liczby według mianownika
Pozostała liczba to 38; liczba 3 pochodzi z pozostałej części poprzedniego etapu, a 8 jest ostatnią cyfrą licznika. Oblicz 38 4 = 9 R2. Ponieważ 4 x 9 = 36, napisz „R2” nad paskiem podziału, ponieważ 38 - 36 = 2.

Krok 5. Zapisz ostateczną odpowiedź
Wynik końcowy i iloraz znajdują się nad paskiem dzielnika. Odpowiedź to 518 4 = 129 R2.
Metoda 3 z 5: Podziel ułamki

Krok 1. Zapisz pytania
Aby podzielić ułamek, po prostu zapisz pierwszy ułamek, a następnie symbol dzielenia, a następnie drugi ułamek.
Na przykład: 3/4 5/8

Krok 2. Odwróć licznik i mianownik drugiej ułamka
Druga frakcja jest teraz odwrotna.
Przykład: 3/4 8/5

Krok 3. Zmień symbol dzielenia na symbol czasów
Aby podzielić ułamek, należy pomnożyć pierwszy ułamek przez odwrotność drugiego.
Przykład: 3/4 x 8/5
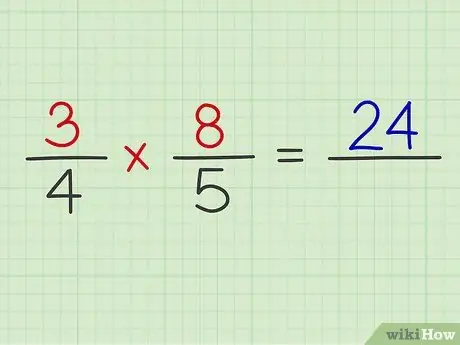
Krok 4. Pomnóż licznik obu ułamków
Po prostu zrób to jak pomnożenie dwóch zwykłych ułamków.
Przykład: 3 x 8 = 24
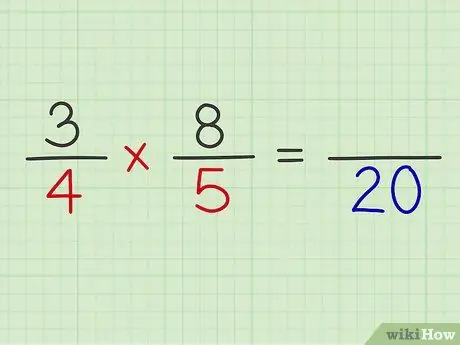
Krok 5. Pomnóż mianowniki obu ułamków
Uzupełnij obliczenia, mnożąc dwa ułamki.
Przykład: 4 x 5 = 20
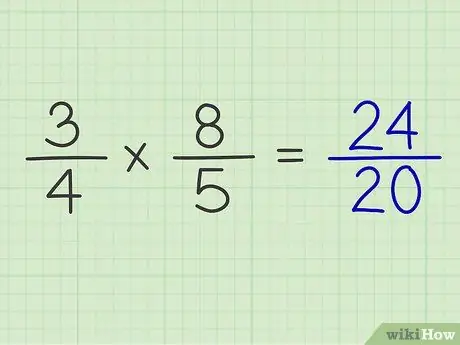
Krok 6. Umieść iloczyn licznika nad iloczynem mianownika
Po pomnożeniu licznika i mianownika dwóch ułamków można uzyskać wynik obliczenia obu ułamków.
Przykład: 3/4 x 8/5 = 24/20

Krok 7. Uprość ułamki
Aby znaleźć największy wspólny czynnik lub największą liczbę, która równo dzieli licznik i mianownik. W tym przypadku największym wspólnym dzielnikiem 24 i 20 jest 4. Aby to udowodnić, zapisz wszystkie liczniki i mianowniki i zakreśl w kółku liczbę największych wspólnych dzielników obu.
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- Ponieważ 4 jest największym wspólnym dzielnikiem 24 i 20, wystarczy podzielić te dwie liczby przez 4, aby uprościć ułamek.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

Krok 8. Przepisz ułamek jako liczbę mieszaną (opcjonalnie)
Sztuczka, wystarczy podzielić licznik przez mianownik i zapisać wynik jako liczbę całkowitą. Następnie wpisz resztę dzielenia jako nowy licznik, a mianownik ułamka się nie zmieni. Ponieważ 6 podzielone przez 5 daje 1 z resztą 1, napisz całą liczbę 1, następnie nowy licznik 1, a następnie mianownik 5, aby otrzymać mieszaną liczbę 1 1/5.
Przykład: 6/5 = 1 1/5
Metoda 4 z 5: Dziel wykładnik

Krok 1. Upewnij się, że wykładniki/potęgi mają tę samą liczbę bazową
Wykładniki można dzielić tylko wtedy, gdy mają tę samą liczbę podstawową. W przeciwnym razie możesz próbować nimi manipulować, aż uzyskasz ten sam numer bazowy.
Przykład: x8 x5

Krok 2. Odejmij wykładnik
Możesz po prostu odjąć pierwszy wykładnik przez drugi. Na razie nie przejmuj się liczbami podstawowymi.
Przykład: 8 - 5 = 3
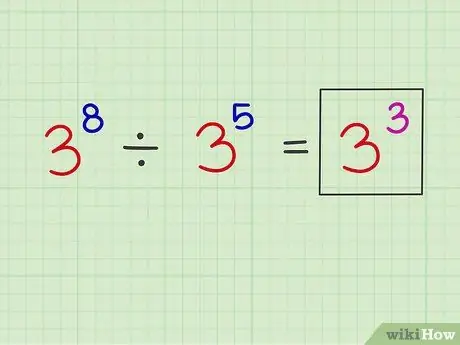
Krok 3. Umieść nowy wykładnik nad oryginalną liczbą podstawową
Teraz możesz zapisać nowy wykładnik nad oryginalną liczbą podstawową.
Przykład: x8 x5 = x3
Metoda 5 z 5: Dzielenie liczb dziesiętnych

Krok 1. Zapisz pytania
Wpisz mianownik (liczbę do podzielenia) poza paskiem dzielnika, a licznik (liczbę do podzielenia) wewnątrz paska dzielnika. W dzieleniu dziesiętnym Twoim celem jest przekształcenie liczby dziesiętnej na liczbę całkowitą.
Przykład: 65,5.5

Krok 2. Zmień mianownik na liczbę całkowitą
Po prostu przesuń kropkę dziesiętną o jedną cyfrę w prawo, aby zmienić 0,5 na 5, czyli 5, 0.

Krok 3. Zmień licznik, przesuwając kropkę dziesiętną o tę samą liczbę cyfr, co mianownik
Ponieważ przesuniesz punkt dziesiętny licznika o jedną cyfrę w prawo, tak aby stał się liczbą całkowitą, punkt dziesiętny mianownika jest również przesunięty o jedną cyfrę w prawo, dzięki czemu 65,5 zmienia się na 655.
Jeśli przesuniesz punkt dziesiętny licznika poza wszystkie jego cyfry, oznacza to, że musisz dodawać zera do cyfr za każdym razem, gdy punkt dziesiętny jest przesuwany. Na przykład, jeśli kropka dziesiętna 7, 2 zostanie przesunięta o trzy cyfry w prawo, liczba zmieni się na 7200, ponieważ dwucyfrowe puste miejsce jest wypełnione zerami

Krok 4. Umieść kropkę dziesiętną na długim pasku podziału tuż nad kropką dziesiętną w liczniku
Ponieważ przesuwasz punkt dziesiętny o jedną cyfrę, aby uzyskać 0,5 liczby całkowitej, dobrym pomysłem jest umieszczenie punktu dziesiętnego nad paskiem podziału dokładnie w miejscu przesunięcia punktu dziesiętnego, tj. za ostatnim 5 na 655.

Krok 5. Rozwiąż problem za pomocą prostego dzielenia długiego
Aby podzielić 655 przez 5, kroki są następujące:
- Podziel cyfrę setek licznika (6) przez mianownik (5). Wynik to 1 z resztą 1. Zapisz liczbę 1 nad dzielnikiem i wpisz 5 pod liczbą 6, która ma być odjęta.
- Pozostała część 1 jest odejmowana od cyfry dziesiątek w liczniku (5) tak, że otrzymujemy 15. Podziel 15 przez 5, aby otrzymać 3. Napisz 3 nad paskiem dzielnika, na prawo od 1.
- Usuń ostatnie 5 cyfr. Podziel 5 przez 5, aby uzyskać 1. Zapisz liczbę 1 nad paskiem dzielnika, na prawo od liczby 3. Nie ma reszty, ponieważ 5 jest podzielne przez 5.
- Odpowiedź długiego dzielenia sekwencyjnego to 655 5 = 131. Wynik ten jest taki sam jak odpowiedź na pytania 65,5 0,5.






