- Autor Jason Gerald [email protected].
- Public 2024-01-19 22:13.
- Ostatnio zmodyfikowany 2025-06-01 06:07.
Matematyka jest trudna. Łatwo jest zapomnieć nawet o podstawowych pojęciach, gdy próbujesz zapamiętać wiele różnych zasad i metod. Oto dwa nowe sposoby uproszczenia ułamków.
Krok
Metoda 1 z 4: Wykorzystanie największego wspólnego czynnika

Krok 1. Zapisz współczynniki licznika i mianownika
Czynniki to liczby, które możesz pomnożyć, aby otrzymać inną liczbę. Na przykład 3 i 4 to dzielniki 12, ponieważ można je pomnożyć, aby otrzymać 12. Aby zapisać czynniki liczby, wystarczy zapisać wszystkie liczby, które można pomnożyć, aby uzyskać tę liczbę, i są one podzielne przez czynniki.
-
Zapisz współczynniki liczby od najmniejszej do największej, nie zapominając o uwzględnieniu współczynnika 1. Na przykład, oto jak zapisać licznik i mianownik ułamka 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Krok 2. Znajdź największy wspólny dzielnik (GCF) licznika i mianownika
GCF to największa liczba, która może równomiernie podzielić dwie lub więcej liczb. Po spisaniu wszystkich czynników liczby wystarczy znaleźć największą liczbę, która jest taka sama na obu listach czynników.
-
24: 1, 2, 3, 4, 6,
Krok 8., 12, 24.
-
32: 1, 2, 4,
Krok 8., 16, 32.
-
GCF 24 i 32 to 8, ponieważ 8 to największa liczba, która może równomiernie podzielić 24 i 32.

Krok 3. Podziel licznik i ułamek przez GCF
Teraz, gdy masz GCF, wszystko, co musisz zrobić, to podzielić licznik i mianownik przez tę liczbę, aby uprościć ułamek do najprostszej postaci. Oto jak to zrobić:
- 24/8 = 3
- 32/8 = 4
- Prosty ułamek to 3/4.

Krok 4. Sprawdź swoją pracę
Jeśli chcesz się upewnić, że poprawnie uprościłeś ułamek, wystarczy pomnożyć nowy licznik i mianownik przez ich GCF, aby odzyskać oryginalny ułamek. Oto jak to zrobić:
- 3 * 8 = 24
- 4 * 8 = 32
-
Wróciłeś do pierwotnej formy, czyli 24/32.
Możesz również sprawdzić ułamek, aby upewnić się, że nie można go dalej uprościć. Ponieważ 3 jest liczbą pierwszą, można ją podzielić tylko przez 1 i samą siebie, a cztery nie są podzielne przez 3, więc ułamek nie może być dalej uproszczony
Metoda 2 z 4: Dziel dalej przez małe liczby

Krok 1. Wybierz małą liczbę
Korzystając z tej metody, na początek wystarczy wybrać niewielką liczbę, taką jak 2, 3, 4, 5 lub 7. Spójrz na ułamki, aby upewnić się, że każda część jest podzielna przez wybraną liczbę. Na przykład, jeśli masz ułamek 24/108, nie wybieraj 5, ponieważ nie są one podzielne przez 5. Jeśli jednak masz ułamek 25/60, 5 jest właściwą liczbą.
Dla ułamka 24/32 2 to dobra liczba. Ponieważ obie liczby są liczbami parzystymi, są one podzielne przez 2

Krok 2. Podziel licznik i mianownik ułamka przez liczbę
Nowy ułamek będzie składał się z nowego licznika i mianownika, które otrzymasz po podzieleniu góry i dołu ułamka 24/32 przez 2. Oto jak to zrobić:
- 24/2 = 12
- 32/2 = 16
- Twoja nowa frakcja to 12/16.
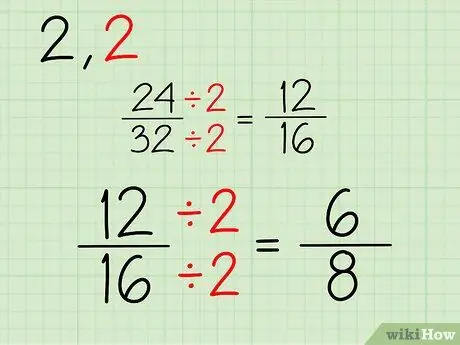
Krok 3. Powtórz
Kontynuuj ten proces. Ponieważ obie liczby są liczbami parzystymi, możesz dalej dzielić przez 2. Jeśli jeden lub oba liczniki i mianowniki są liczbami nieparzystymi, możesz spróbować podzielić przez inną liczbę. Oto proces upraszczania frakcji 12/16:
- 12/2 = 6
- 16/2 = 8
- Twoja nowa frakcja to 6/8.

Krok 4. Kontynuuj dzielenie liczby, aż przestanie być podzielna
Nowy licznik i mianownik są również liczbami parzystymi, więc możesz dalej dzielić przez 2. Oto jak to zrobić:
- 6/2 = 3
- 8/2 = 4
- Twoja nowa frakcja to 3/4.

Krok 5. Upewnij się, że ułamek nie może być dalej upraszczany
W ułamku 3/4 3 jest liczbą pierwszą, więc dzielniki wynoszą tylko 1 i samo, a 4 nie jest podzielne przez 3, więc ułamek nie może być dalej upraszczany. Jeśli licznika lub mianownika ułamka nie można już dzielić przez wybraną liczbę, nadal możesz podzielić go przez inną liczbę.
Na przykład, jeśli masz ułamek 10/40 i podzielisz licznik i mianownik przez 5, wynik to 2/8. Nie możesz dalej dzielić licznika i ułamka przez 5, ale możesz podzielić oba przez 2, więc wynik końcowy to 1/4

Krok 6. Sprawdź swoją pracę
Ponownie pomnóż 3/4 przez 2/2 trzy razy, aby upewnić się, że uzyskasz początkowy ułamek, czyli 24/32. Oto jak to zrobić:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Zauważ, że dzielisz 24/32 przez 2 * 2 * 2, co jest tym samym, co dzielenie przez 8, największy GCF z 24 i 32.
Metoda 3 z 4: Zapisywanie czynników

Krok 1. Zapisz swoją frakcję
Zostaw sporą przestrzeń po prawej stronie kartki - będziesz potrzebować jej do zapisania współczynników.

Krok 2. Zapisz współczynniki licznika i mianownika
Same czynniki z dwóch. Najłatwiej jest pisać czynniki jeden na drugim. Zacznij od cyfry 1 i zapisz współczynniki.
-
Na przykład, jeśli twoja frakcja to 24/60, zacznij od 24.
Zapisz: 24 -- 1, 2, 3, 4, 6, 8, 12, 24
-
Następnie liczba 60.
Zapisz: 60 -- 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Krok 3. Znajdź i podziel przez największy wspólny czynnik
Ten termin może być zapisany jako GCF w drukowanej książce. Jaka jest największa liczba dzieląca licznik i mianownik? Niezależnie od liczby, podziel obie liczby przez tę liczbę.
W naszym przykładzie największą liczbą, która jest dzielnikiem obu liczb, jest 12. Zatem dzielimy 24 przez 12 i 60 przez 12, co daje nam 2/5 - nasz ułamek prosty
Metoda 4 z 4: Korzystanie z drzewa czynników pierwszych

Krok 1. Znajdź czynniki pierwsze licznika i mianownika
Liczba pierwsza to liczba, której nie można podzielić przez żadną inną liczbę (inną niż sama i 1 oczywiście). 2, 3, 5, 7 i 11 to przykłady liczb pierwszych.
- Zacznij od licznika. Od 24 podziel na 2 i 12. Ponieważ 2 jest już liczbą pierwszą, nie musisz jej już dzielić! Następnie podziel 12 na 2 liczby: 2 i 6. 2 to liczby pierwsze - świetnie! Teraz podziel 6 na 2 liczby: 2 i 3. Teraz masz 2, 2, 2 i 3 jako liczby pierwsze.
- Teraz pracuj nad mianownikiem. Od 60 podziel swoje drzewo na 2 i 30. 30 następnie podziel na 2 i 15. Następnie podziel 15 na 3 i 5, które są liczbami pierwszymi. Teraz masz 2, 2, 3 i 5 jako liczby pierwsze.
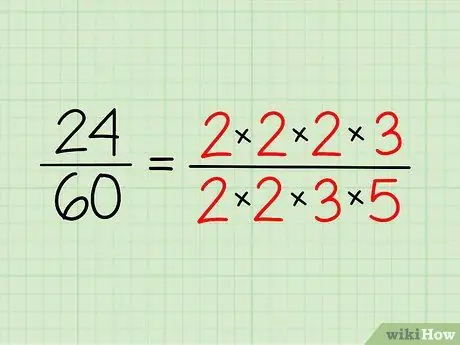
Krok 2. Zapisz rozkład na czynniki pierwsze każdej liczby
Zapisz liczby pierwsze, które masz dla każdej liczby i zapisz je w formie mnożenia. Nie musisz tego mnożyć - to tylko sposób na to, żeby było łatwiej zobaczyć.
- Tak więc dla 24 masz 2 x 2 x 2 x 3 = 24.
- Za 60 masz 2 x 2 x 3 x 5 = 60

Krok 3. Wyeliminuj te same czynniki
Każda liczba będąca częścią obu liczb może zostać odrzucona. W tym przykładzie równe czynniki to para 2 i jeden 3. Do widzenia!
- Reszta to 2 i 5 - lub 2/5! Tę samą odpowiedź otrzymaliśmy powyżej.
- Jeśli licznik i mianownik ułamka są liczbami parzystymi, nie dziel po prostu przez dwa. Kontynuuj dzielenie, aż uzyskana liczba nie będzie mogła zostać ponownie podzielona.






