- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:15.
- Ostatnio zmodyfikowany 2025-01-23 12:42.
Przemieszczenie w fizyce oznacza zmianę położenia obiektu. Obliczając przemieszczenie, obliczasz odległość obiektu na podstawie jego początkowej i końcowej lokalizacji. Formuła, której używasz do obliczania przemieszczenia, zależy od zmiennej podanej w zadaniu. Wykonaj poniższe czynności, aby obliczyć przemieszczenie.
Krok
Część 1 z 5: Obliczanie wynikowego przemieszczenia

Krok 1. Użyj wzoru na wynikowe przemieszczenie, jeśli jednostka odległości jest używana do wskazania lokalizacji początkowej i końcowej
Chociaż odległość różni się od przemieszczenia, wynikowy problem przemieszczenia sprawdza, ile kilometrów lub metrów przebył obiekt. Użyjesz tej jednostki miary, aby obliczyć przemieszczenie i jak daleko położenie obiektu odbiega od jego punktu początkowego.
- Wzór na wypadkowe przemieszczenie jest zapisany jako: S = x²+y². S to przemieszczenie. X to pierwszy kierunek ruchu obiektu, a Y to drugi kierunek ruchu obiektu. Jeśli twój obiekt porusza się tylko w jednym kierunku, to Y = 0.
- Obiekt może poruszać się tylko w dwóch kierunkach, ponieważ ruch wzdłuż osi północ/południe lub wschód/zachód jest uważany za ruch neutralny.

Krok 2. Połącz kropki w kolejności ruchu i oznacz je od A do Z
Użyj linijki, aby narysować linię prostą od punktu do punktu.
- Pamiętaj również, aby połączyć punkt początkowy z punktem końcowym za pomocą linii prostej. To jest przemieszczenie, które obliczymy.
- Na przykład, jeśli obiekt przesunie się na wschód 300 mi północ 400 m, utworzy trójkąt prostokątny. AB będzie pierwszą odnogą trójkąta, a BC drugą odnogą. AC będzie przeciwprostokątną trójkąta, a jej wielkość będzie przemieszczeniem obiektu. W tym przykładzie dwa kierunki to wschód i północ.

Krok 3. Wprowadź wartości dla x² i y²
Teraz, gdy znasz dwa kierunki ruchu swojego obiektu, wprowadź wartości do odpowiednich zmiennych.
Na przykład x = 300 i y = 400. Twoja formuła powinna wyglądać tak: S = 300² + 400²
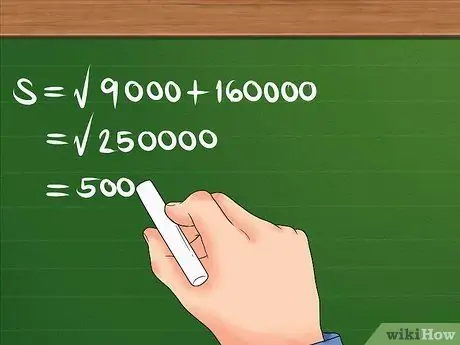
Krok 4. Oblicz formułę używając kolejności operacji
Najpierw kwadrat 300 i 400, następnie dodaj je i znajdź pierwiastek kwadratowy z sumy.
Na przykład: S = 90000 + 160000. S = 250000. S = 500. Teraz wiesz, że przemieszczenie wynosi 500 m
Część 2 z 5: Kiedy znana jest prędkość i czas

Krok 1. Użyj tego wzoru, gdy problem określa prędkość obiektu i czas potrzebny
Niektóre problemy matematyczne nie powiedzą Ci, jak daleko lub jak szybko porusza się obiekt. Możesz obliczyć przemieszczenie, używając tej wielkości czasu i prędkości.
-
W takim przypadku formuła staje się: S = 1/2(u + v)t.
U = prędkość początkowa obiektu, czyli jak szybko obiekt zaczyna poruszać się w określonym kierunku. V = prędkość końcowa obiektu lub szybkość, z jaką obiekt porusza się w kierunku ostatecznego położenia. T = czas, jaki zajmuje obiektowi dotarcie do ostatecznej lokalizacji.
- Przykład: Samochód jedzie drogą przez 45 sekund (wymagany czas). Samochód skręca na zachód z prędkością 20 m/s (prędkość początkowa), a na końcu drogi jego prędkość wynosi 23 m/s (prędkość końcowa). Oblicz przemieszczenie na podstawie tych czynników.

Krok 2. Wprowadź żądaną prędkość i czas do odpowiednich zmiennych
Teraz, gdy wiesz, jak daleko porusza się samochód, jak szybko porusza się samochód na początku i na końcu, możesz określić odległość od lokalizacji początkowej do lokalizacji końcowej.
Twoja formuła powinna wyglądać tak: S = 1/2(20 + 23)45

Krok 3. Oblicz formułę po umieszczeniu wartości we właściwym miejscu
Pamiętaj, aby postępować zgodnie z kolejnością operacji, w przeciwnym razie przemieszczenia dadzą bardzo różne wartości.
- W przypadku tej formuły nie ma znaczenia, czy przypadkowo zamienisz prędkość początkową i końcową. Ponieważ najpierw dodasz te liczby do siebie, nie ma znaczenia, gdzie są w nawiasach. Jednak w przypadku innych wzorów zamiana prędkości początkowej i końcowej spowoduje uzyskanie różnych wartości przemieszczenia.
- Twoja formuła powinna wyglądać tak: S = 1/2(43)45. Najpierw podziel 43 przez 2, co daje 21,5. Następnie pomnóż 21,5 przez 45, aby otrzymać 967,5 metra. 967, 5 to wielkość przemieszczenia, czyli jak daleko samochód oddalił się od punktu początkowego.
Część 3 z 5: Kiedy znana jest początkowa prędkość, przyspieszenie i czas
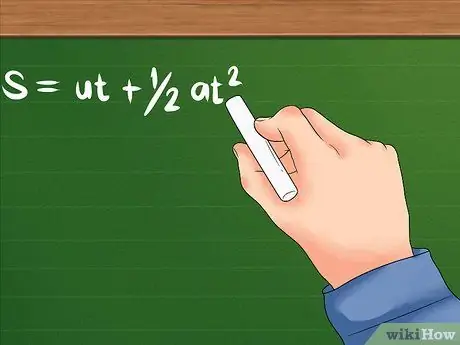
Krok 1. Użyj zmodyfikowanego wzoru, gdy oprócz początkowej prędkości i czasu znane jest przyspieszenie
Niektóre pytania powiedzą ci tylko, jak szybko obiekt porusza się na początku, jak szybko obiekt zaczyna przyspieszać i jak daleko się porusza. Będziesz potrzebować następującej formuły.
- Wzór na ten problem to: S = ut + 1/2at². U nadal wskazuje prędkość początkową; a jest przyspieszeniem obiektu, czyli jak szybko zaczyna się zmieniać jego prędkość. T może oznaczać czas potrzebny do przyspieszenia lub określony czas potrzebny obiektowi na przyspieszenie. Oba będą używać jednostek czasu, takich jak sekundy, godziny i inne.
- Załóżmy, że samochód poruszający się z prędkością 25 m/s (prędkość początkowa) zaczyna przyspieszać z prędkością 3 m/s2 (przyspieszenie) przez 4 sekundy (czas). Jaka jest przemieszczenie auta po 4 sekundach?

Krok 2. Wprowadź wartości w formule
W przeciwieństwie do poprzedniej formuły, tutaj reprezentowana jest tylko prędkość początkowa, więc upewnij się, że wprowadziłeś poprawne dane.
W oparciu o powyższe przykładowe dane formuła wyglądałaby tak: S = 25(4) + 1/2(3)4². Pomaga dodać nawiasy wokół wartości przyspieszenia i czasu, aby pomóc Ci rozdzielić liczby
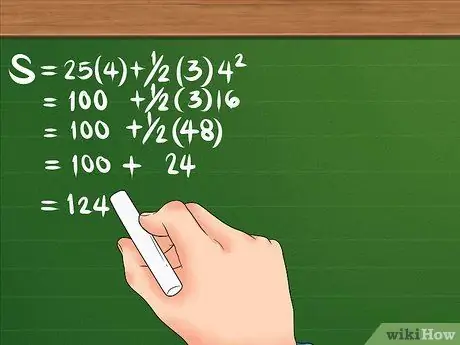
Krok 3. Oblicz przemieszczenie, wykonując je w odpowiedniej kolejności operacji
Szybkim sposobem na zapamiętanie sekwencji operacji jest most osioł Kur ir Kua ci Kadang Ba wa Juragan Turtles. Reprezentuje prawidłową kolejność: nawiasy, kwadraty, mnożenie, dzielenie, dodawanie i odejmowanie.
Spójrzmy ponownie na wzór: S = 25(4) + 1/2(3)4². Najpierw kwadrat 4, wynik to 16. Następnie pomnóż 16 przez 3, co daje 48; potem również pomnóż 25 przez 4, by otrzymać 100. Podziel 48 przez 2, by otrzymać 24. Twoje równanie powinno wyglądać tak: S = 100 + 24. Po dodaniu tych dwóch razem przemieszczenie wynosi 124 metry
Część 4 z 5: Obliczanie przemieszczenia kątowego

Krok 1. Znajdź przemieszczenie kątowe, gdy obiekt porusza się po torze kołowym
Chociaż nadal będziesz obliczać przemieszczenie za pomocą linii prostej, musisz znaleźć różnicę między początkową i końcową lokalizacją obiektu, gdy porusza się on po torze kołowym.
- Wyobraź sobie dziewczynę siedzącą na karuzeli. Obracając się z karuzelą, porusza się po torze kołowym. Przemieszczenie kątowe próbuje znaleźć najkrótszą odległość między początkową i końcową lokalizacją, gdy obiekt nie porusza się w linii prostej.
- Wzór na przemieszczenie kątowe to: = S/r, gdzie S jest przemieszczeniem liniowym, r jest promieniem i jest przemieszczeniem kątowym. Przemieszczenie liniowe określa, jak daleko obiekt porusza się po łuku. Promień to odległość obiektu od środka okręgu. Przemieszczenie kątowe to wartość, którą chcemy znaleźć.

Krok 2. Wstaw do równania przemieszczenie liniowe i promień
Pamiętaj, że promień to odległość od środka okręgu; niektóre problemy podpowiedzą ci średnicę koła, którą należy podzielić przez 2, aby znaleźć promień.
- Oto przykładowy problem: dziewczyna jeździ na karuzeli. Siedzisko znajduje się 1 metr od środka koła (promień). Jeśli dziewczyna porusza się po łuku 1,5 metra (przemieszczenie liniowe), jakie jest jej przesunięcie kątowe?
- Twoje równanie będzie wyglądać tak: = 1,5/1.
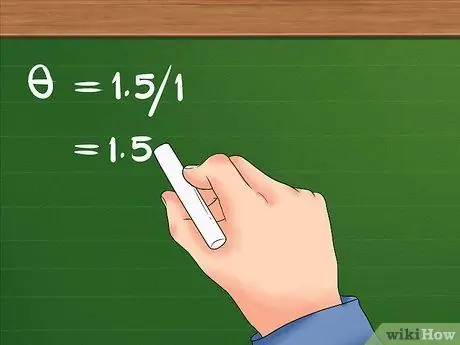
Krok 3. Podziel przemieszczenie liniowe przez promień
Podział ten spowoduje przemieszczenie kątowe obiektu.
- Po podzieleniu 1,5 przez 1 otrzymujemy 1,5 Przemieszczenie kątowe dziewczynki wynosi 1,5 radiany.
- Ponieważ przemieszczenie kątowe mierzy, jak bardzo obiekt obraca się od swojej pozycji początkowej, należy je mierzyć jako kąt, a nie odległość. Radian to jednostka używana do pomiaru kątów.
Część 5 z 5: Zrozumienie migracji
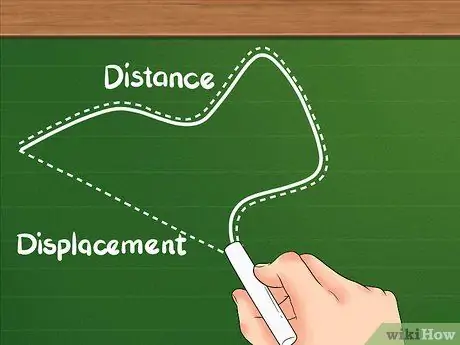
Krok 1. Wiedz, że odległość ma inną definicję niż przemieszczenie
Odległość pokazuje, jak daleko jest całkowita odległość przebyta przez obiekt.
- Odległość jest często nazywana wielkością skalarną. Odległość pokazuje odległość przebytą przez obiekt niezależnie od kierunku obiektu.
- Na przykład, jeśli przejdziesz 2 kroki na wschód, 2 kroki na południe, 2 kroki na zachód, a następnie 2 kroki na północ, powrócisz do swojej pozycji wyjściowej. Nawet jeśli przeszedłeś przez całość dystans 10 kroków dalej, po prostu ruszaj się 0 kroków, ponieważ twoja ostateczna lokalizacja jest taka sama, jak twoja początkowa lokalizacja (twoja ścieżka przypomina pudełko).

Krok 2. Zrozum, że przemieszczenie jest różnicą między dwoma lokalizacjami
Przemieszczenie nie jest całkowitą sumą ruchu, jak odległość; zmiany koncentrują się na obszarze między lokalizacją początkową i końcową.
- Przemieszczenie nazywa się wielkością wektorową i pokazuje zmianę położenia obiektu, biorąc pod uwagę kierunek ruchu obiektu.
- Na przykład idziesz na wschód przez 5 kroków. Jeśli cofniesz się o 5 kroków na zachód, poruszysz się w kierunku przeciwnym do swojej pierwotnej lokalizacji. Mimo że pokonałeś 10 kroków, Twoja pozycja się nie zmieniła; twoje przemieszczenie wynosi 0 kroków.

Krok 3. Zapamiętaj słowa „do przodu” i „do tyłu”, kiedy próbujesz wyobrazić sobie przemieszczenie
Poruszanie się w przeciwnym kierunku eliminuje przemieszczenie obiektu.
Wyobraź sobie trenera piłki nożnej tam iz powrotem na uboczu. Kiedy krzyczał na graczy, kilkakrotnie przesunął się z lewej strony na prawą. Jeśli obserwujesz go, gdy porusza się od lewej do prawej, obserwujesz całkowitą odległość, którą przebył. Załóżmy jednak, że trener zatrzymuje się, aby porozmawiać z rozgrywającym na linii bocznej. Jeśli znajduje się w innym miejscu niż jego początkowa lokalizacja przed przeniesieniem, obserwujesz ruch trenera

Krok 4. Wiedz, że przemieszczenie jest mierzone przy użyciu prostej ścieżki, a nie ścieżki kołowej
Aby znaleźć przemieszczenie, musisz znaleźć najkrótszy i najbardziej efektywny sposób obliczenia różnicy między dwoma punktami.
- Ścieżka okrężna zabierze Cię z początkowej lokalizacji do ostatecznej lokalizacji, ale nie jest to najkrótsza ścieżka. Aby pomóc sobie to zwizualizować, wyobraź sobie, że idziesz w linii prostej i natrafiasz na filar. Nie możesz przebić się przez ten filar, więc omijasz go. Nawet jeśli twoja ostateczna pozycja jest taka sama, jak w przypadku przebicia się przez filar, będziesz potrzebować dodatkowych kroków, aby osiągnąć ten cel.
- Chociaż przemieszczenie reprezentuje prostą ścieżkę, wiedz, że możesz zmierzyć przemieszczenie obiektu, który jest obecnie poruszać się po ścieżce kołowej. To przemieszczenie nazywa się przemieszczeniem kątowym i można je obliczyć, znajdując najkrótszą drogę od lokalizacji początkowej do lokalizacji końcowej.

Krok 5. Wiedz, że przemieszczenie może być ujemne, w przeciwieństwie do odległości
Jeśli twoja ostateczna lokalizacja zostanie osiągnięta, poruszając się w przeciwnym kierunku do początkowego, to twoje przemieszczenie jest ujemne.
- Na przykład idziemy 5 kroków na wschód, a następnie 3 kroki na zachód. Nawet jeśli w obliczeniach poruszasz się o 2 kroki od swojej pozycji początkowej, Twoje przemieszczenie wynosi -2, ponieważ poruszasz się w przeciwnym kierunku. Twój dystans zawsze będzie dodatni, ponieważ nie możesz liczyć wstecz w krokach, kilometrach i tak dalej.
- Ujemne przemieszczenie nie oznacza, że przemieszczenie się zmniejsza. Negatywny oznacza po prostu kierunek przeciwny.

Krok 6. Zdaj sobie sprawę, że czasami odległość i przemieszczenie mogą być takie same
Jeśli pójdziesz prosto przez 25 kroków i zatrzymasz się, pokonana odległość będzie równa przesunięciu z pierwotnej lokalizacji.
- Dotyczy to tylko sytuacji, gdy przenosisz się z jednej lokalizacji z pozycji początkowej w linii prostej. Na przykład mieszkasz w San Francisco w Kalifornii i dostajesz nową pracę w Las Vegas w stanie Nevada. Musisz przeprowadzić się do Las Vegas, aby być blisko swojej pracy. Jeśli wsiądziesz do samolotu, który leci? prosty z San Francisco do Las Vegas przejedziesz tę samą odległość i przemieszczenie x.
- Jeśli jednak jedziesz z San Francisco do Las Vegas, przejedziesz odległość x, ale odległość y. Ponieważ jazda samochodem zwykle ma różne kierunki (na wschód od tej drogi, na zachód od tej drogi), będziesz podróżować na dłuższych dystansach niż najkrótsza odległość między dwoma miastami.






