- Autor Jason Gerald [email protected].
- Public 2024-01-19 22:13.
- Ostatnio zmodyfikowany 2025-06-01 06:07.
Siła wyporu to siła przeciwna do grawitacji, która oddziałuje na wszystkie obiekty zanurzone w płynie. Kiedy przedmiot jest umieszczony w płynie, masa przedmiotu naciska na płyn (ciecz lub gaz), podczas gdy siła wyporu popycha przedmiot wbrew grawitacji. Ogólnie rzecz biorąc, tę siłę wyporu można obliczyć za pomocą równania Fa = VT × × g, z Fa jest siła wyporu, VT to objętość zanurzonego obiektu, to gęstość płynu, a g to siła grawitacyjna. Aby dowiedzieć się, jak określić pływalność obiektu, zapoznaj się z krokiem 1 poniżej, aby rozpocząć.
Krok
Metoda 1 z 2: Wykorzystanie równania wyporu
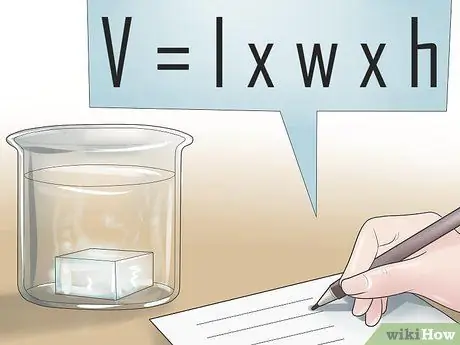
Krok 1. Znajdź objętość zanurzonej części obiektu
Siła wyporu działająca na obiekt jest proporcjonalna do objętości zanurzonego obiektu. Innymi słowy, im większa jest zanurzona, stała część obiektu, tym większa siła wyporu działająca na obiekt. Oznacza to, że przedmioty zanurzone w cieczy mają siłę wyporu, która wypycha przedmiot w górę. Aby rozpocząć obliczanie siły wyporu działającej na obiekt, pierwszym krokiem jest zwykle określenie objętości obiektu zanurzonego w płynie. Dla równania wyporu wartość ta powinna być w metrach3.
- W przypadku obiektu całkowicie zanurzonego w płynie objętość zanurzona jest równa objętości samego obiektu. W przypadku obiektów unoszących się nad powierzchnią płynu obliczana jest tylko objętość pod powierzchnią.
- Załóżmy na przykład, że chcemy znaleźć siłę wyporu działającą na gumową kulkę unoszącą się na wodzie. Jeśli gumowa kulka jest idealną kulą o średnicy 1 mi pływa, a jej połowa jest zanurzona pod wodą, możemy obliczyć objętość zanurzonej części, znajdując całkowitą objętość kuli i dzieląc ją przez dwa. Ponieważ objętość kuli wynosi (4/3) (promień)3 wiemy, że objętość naszej kuli wynosi (4/3)π(0, 5)3 = 0,524 metra3. 0, 524/2 = 0,262 metra3 tonąć.

Krok 2. Znajdź gęstość płynu
Kolejnym krokiem w procesie wyznaczania wyporu jest określenie gęstości (w kilogramach/metr).3) płynu, w którym zanurzony jest przedmiot. Gęstość to miara masy obiektu lub substancji w stosunku do jego objętości. Jeśli dane są dwa obiekty o tej samej objętości, obiekt o większej gęstości będzie miał większą masę. Zgodnie z regułą, im większa gęstość płynu, w którym zanurzony jest przedmiot, tym większa siła wyporu. W przypadku płynów zwykle najłatwiejszym sposobem określenia gęstości jest po prostu sprawdzenie jej w materiale odniesienia.
- W naszym przykładzie nasza piłka unosi się w wodzie. Zaglądając do źródeł akademickich, możemy stwierdzić, że woda ma gęstość około. 1000 kilogramów/metr3.
- Inne powszechnie stosowane gęstości płynów są wymienione w źródłach inżynierskich. Jedną z list można znaleźć tutaj.
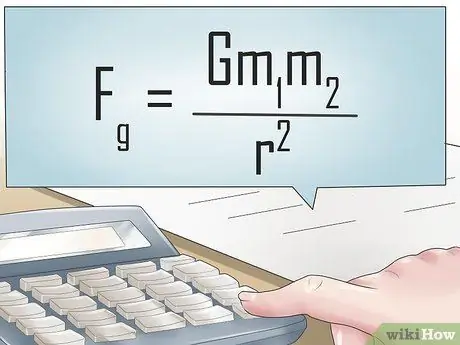
Krok 3. Znajdź siłę grawitacji (lub inną siłę skierowaną w dół)
Niezależnie od tego, czy obiekt tonie, czy unosi się w płynie, zawsze ma siłę grawitacyjną. W świecie rzeczywistym stała siły skierowanej w dół jest równa 9,81 niutonów/kilogram. Jednak w sytuacjach, w których na płyn i zanurzony w nim obiekt działają inne siły, takie jak siła odśrodkowa, należy również wziąć pod uwagę tę siłę, aby określić wypadkową siłę skierowaną w dół dla całego układu.
- W naszym przykładzie pracujemy ze zwykłym, statycznym układem, więc możemy założyć, że jedyną skierowaną w dół siłą działającą na płyny i obiekty jest ogólna siła grawitacyjna - 9,81 niutonów/kilogram.
- Co jednak, jeśli nasza piłka, która unosi się w wiadrze z wodą, porusza się po okręgu w kierunku poziomym z dużą prędkością? W tym przypadku, zakładając, że wiadro jest obracane wystarczająco szybko, aby woda i kulka się nie rozlewały, siła skierowana w dół w tej sytuacji będzie pochodzić z siły odśrodkowej wytworzonej przez ruch wiadra, a nie z ziemskiej grawitacji.

Krok 4. Pomnóż objętość × gęstość × grawitacja
Jeśli masz wartość objętości swojego obiektu (w metrach)3), gęstość płynu (w kilogramach/metr3) oraz siła grawitacji (siła działająca w dół systemu), więc znalezienie wyporu jest bardzo łatwe. Wystarczy pomnożyć te trzy wartości, aby znaleźć siłę wyporu w niutonach.
Rozwiążmy nasz przykładowy problem, wstawiając nasze wartości do równania Fa = VT × × g. Fa = 0,262 metra3 × 1000 kilogramów/metr3 × 9,81 niutonów/kilogram = 2570 niutonów.

Krok 5. Sprawdź, czy twój obiekt unosi się, porównując wypór z siłą grawitacji
Korzystając z równania wyporu, łatwo jest znaleźć siłę, która wypycha obiekt w górę i na zewnątrz płynu. Jednak przy odrobinie dodatkowego wysiłku można również określić, czy przedmiot unosi się, czy tonie. Po prostu znajdź siłę wyporu dla całego obiektu (innymi słowy, użyj całej objętości jako wartości VT), a następnie znajdź siłę grawitacyjną popychającą ją w dół za pomocą równania G = (masa obiektu) (9,81 metra/sekundę2). Jeśli siła wyporu jest większa niż siła grawitacji, obiekt unosi się. Z drugiej strony, jeśli siła grawitacji jest większa niż siła wyporu, obiekt zatonie. Jeśli jasności są takie same, mówi się, że obiekt unosi się.
-
Na przykład, powiedzmy, że chcemy wiedzieć, czy drewniana cylindryczna beczka o masie 20 kilogramów, średnicy 0,75 mi wysokości 1,25 m będzie pływać w wodzie. Ten problem będzie wymagał kilku kroków:
- Objętość możemy znaleźć ze wzoru na objętość cylindra V = (promień)2(wysoka). V = (0, 375)2(1, 25) = 0,55 metra3.
- Następnie, zakładając, że siła grawitacji jest zwykła, a wody o zwykłej gęstości, możemy znaleźć siłę wyporu beczki. 0,55 metra3 × 1000 kilogramów/metr3 × 9,81 niutonów/kilogram = 5395, 5 niutonów.
- Teraz musimy znaleźć siłę grawitacji beczki. G = (20 kg) (9,81 metra/sekundę)2) = 196,2 niutonów. Ta siła jest mniejsza niż siła wyporu, więc lufa będzie się unosić.

Krok 6. Użyj tego samego podejścia, jeśli twój płyn jest gazem
Pracując nad problemami z pływalnością nie zapominaj, że płyn, w którym zanurzony jest obiekt, nie musi być płynem. Gazy są również płynami i chociaż gazy mają bardzo niską gęstość w porównaniu z innymi substancjami, nadal mogą podtrzymywać pewne masy obiektów unoszących się w gazie. Prosty balon z helem jest tego dowodem. Ponieważ gaz w balonie jest mniej gęsty niż otaczający go płyn (powietrze otoczenia), balon unosi się!
Metoda 2 z 2: Wykonywanie prostego eksperymentu z pływalnością

Krok 1. Umieść małą miskę lub filiżankę w większej misce
W przypadku niektórych artykułów gospodarstwa domowego łatwo jest zaobserwować zasady pływalności w eksperymencie! W tym prostym eksperymencie zademonstrujemy, że zanurzony obiekt doświadcza siły wyporu, ponieważ wypiera objętość płynu równą objętości zanurzonego obiektu. Kiedy to zrobimy, za pomocą tego eksperymentu zademonstrujemy również praktyczny sposób na znalezienie siły wyporu obiektu. Na początek umieść mały, otwarty pojemnik, taki jak miska lub filiżanka, w większym pojemniku, takim jak duża miska lub wiadro.

Krok 2. Napełnij mały pojemnik po brzegi
Następnie napełnij mniejszy wewnętrzny pojemnik wodą. Chcesz, aby woda była tak wysoka, jak pojemnik, bez rozlewania. Bądź ostrożny tutaj! Jeśli rozlejesz wodę, opróżnij większy pojemnik, zanim spróbujesz ponownie.
- Na potrzeby tego eksperymentu można założyć, że woda ma ogólną gęstość 1000 kilogramów/metr3. O ile nie używasz wody morskiej lub zupełnie innej cieczy, większość rodzajów wody ma prawie taką samą gęstość jak ta wartość referencyjna, więc niewielka różnica nie zmieni naszych wyników.
- Jeśli masz krople do oczu, może to być bardzo przydatne do podniesienia poziomu wody w małym pojemniku.

Krok 3. Zanurz mały przedmiot
Następnie poszukaj małego przedmiotu, który zmieści się do małego pojemnika i nie zostanie uszkodzony przez wodę. Znajdź masę tego obiektu w kilogramach (możesz użyć wagi lub wagi, która może mierzyć gramy i przeliczać je na kilogramy). Następnie, nie mocząc palców, powoli, ale zdecydowanie zanurz przedmiot w wodzie, aż zacznie unosić się na wodzie lub możesz go lekko przytrzymać, a następnie puścić. Zauważysz, że część wody z małego pojemnika wyleje się do zewnętrznego pojemnika.
Na potrzeby naszego przykładu załóżmy, że w małym pojemniku zanurzamy samochodzik-zabawkę o masie 0,05 kilograma. Nie musimy znać objętości tego samochodu, aby obliczyć jego wyporność, ponieważ zobaczymy to w następnym kroku

Krok 4. Zbierz i policz rozlaną wodę
Gdy zanurzysz przedmiot w wodzie, wypiera część wody - w przeciwnym razie nie będzie miejsca na umieszczenie przedmiotu w wodzie. Kiedy obiekt wypycha wodę, woda odpycha się, tworząc siłę wyporu. Wylej rozlaną wodę z małego pojemnika i wlej ją do małej miarki. Objętość wody w miarce jest równa objętości zanurzonego obiektu.
Innymi słowy, jeśli twój przedmiot unosi się, objętość wody, która się wylewa, będzie równa objętości przedmiotu zanurzonego pod powierzchnią wody. Jeśli twój obiekt tonie, objętość wylewającej się wody jest równa całkowitej objętości obiektu

Krok 5. Oblicz masę rozlanej wody
Skoro znasz gęstość wody i możesz zmierzyć objętość wody, która rozlewa się w miarce, możesz obliczyć jej masę. Po prostu zmień głośność na metry3 (pomoc w konwersji online, jak ta, może pomóc) i pomnóż przez gęstość wody (1000 kilogramów/metr3).
W naszym przykładzie załóżmy, że nasz samochodzik tonie w małym pojemniku i porusza się o około dwie łyżki stołowe (0,0003 metra)3). Aby obliczyć masę naszej wody, pomnożymy ją przez jej gęstość: 1000 kilogramów/metr3 × 0,0003 metra3 = 0,03 kilograma.

Krok 6. Porównaj masę rozlanej wody z masą przedmiotu
Teraz, gdy znasz masę obiektu, który zanurzasz w wodzie, oraz masę rozlanej wody, porównaj je, aby zobaczyć, która masa jest większa. Jeśli masa przedmiotu zanurzonego w małym pojemniku jest większa niż rozlanej wody, przedmiot zatonie. Z drugiej strony, jeśli masa rozlanej wody jest większa, obiekt będzie się unosił. Na tym polega zasada wyporu w doświadczeniu - aby obiekt mógł unosić się na wodzie, musi wypierać ilość wody o masie większej niż masa samego obiektu.
- Zatem obiekty o małej masie, ale dużej objętości to obiekty, które najłatwiej unoszą się na wodzie. Ta właściwość oznacza, że puste obiekty bardzo łatwo unoszą się w powietrzu. Wyobraź sobie kajak - kajak dobrze pływa, ponieważ jest pusty w środku, dzięki czemu może przenosić dużo wody bez konieczności posiadania dużej masy. Jeśli czółno nie jest puste (solidne), to nie będzie prawidłowo pływać.
- W naszym przykładzie samochód ma większą masę (0,05 kilograma) niż rozlana woda (0,03 kilograma). Zgadza się to z tym, co obserwujemy: samochody toną.






