- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:21.
- Ostatnio zmodyfikowany 2025-06-01 06:07.
Dodawanie i odejmowanie ułamków to ważna umiejętność. Ułamki pojawiają się cały czas w życiu codziennym, zwłaszcza na lekcjach matematyki, od podstawówki po studia. Wykonaj poniższe czynności, aby dowiedzieć się, jak dodawać i odejmować ułamki od ułamków równoważnych, ułamków nierównych, liczb mieszanych lub ułamków wspólnych. Jeśli znasz już jeden sposób, naprawdę łatwo rozwiązać pozostałe ułamki!
Krok
Metoda 1 z 4: Dodawanie i odejmowanie ułamków o tym samym mianowniku
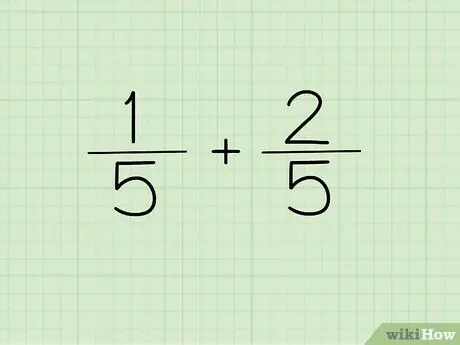
Krok 1. Zapisz swoje pytanie
Jeśli mianownik dwóch ułamków, które chcesz dodać lub odjąć, jest taki sam, zapisz mianownik raz jako mianownik odpowiedzi.
Innymi słowy, 1/5 i 2/5 nie muszą być zapisywane jako 1/5 + 2/5 = ?, ale można zapisać jako (1+2)/5 = ?. Mianowniki są takie same, więc można je zapisać tylko raz. Dwa liczniki są połączone
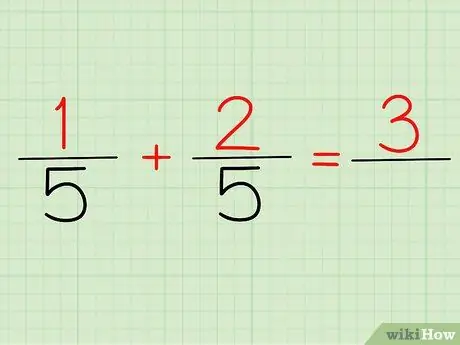
Krok 2. Dodaj liczniki
Licznik to liczba, która znajduje się powyżej dowolnego ułamka. Jeśli spojrzymy na powyższy problem, 1/5 i 2/5, 1 i 2 to nasze liczniki.
Niezależnie od tego, czy napiszesz 1/5 + 2/5 czy (1+2)/5, twoja odpowiedź będzie taka sama: 3! Ponieważ 1 + 2 = 3

Krok 3. Zostaw mianownik
Ponieważ mianowniki są takie same, nie rób nic z mianownikami! Nie dodawać, odejmować, mnożyć ani dzielić. Niech będzie.
Tak więc, z tego samego przykładu, naszym mianownikiem jest 5. Tak! 5 to najniższa liczba naszej frakcji. Mamy połowę odpowiedzi

Krok 4. Zapisz swoją odpowiedź
Teraz wszystko, co musisz zrobić, to zapisać swój licznik i mianownik! Jeśli użyjesz powyższego przykładu, twoja odpowiedź będzie 3/5.
Jaki jest twój licznik? 3. Twój mianownik? 5. Zatem 1/5 + 2/5 lub (1+2)/5 równa się 3/5.
Metoda 2 z 4: Dodawanie i odejmowanie ułamków o różnych mianownikach

Krok 1. Znajdź najmniej wspólny mianownik
Oznacza to, że najmniejszy mianownik jest taki sam dla obu ułamków. Załóżmy, że mamy ułamki 2/3 i 3/4. Jaki jest mianownik? 3 i 4. Aby znaleźć najmniejszy wspólny mianownik obu ułamków, możesz to zrobić na trzy sposoby:
- Zapisz wielokrotności. Wielokrotności 3 to 3, 6, 9, 12, 15, 18… i tak dalej. Wielokrotność 4? 4, 8, 12, 16, 20 i tak dalej. Jaka jest najmniejsza liczba będąca wielokrotnością tych dwóch? 12! To najmniejszy wspólny mianownik.
-
Rozkład na czynniki pierwsze. Jeśli znasz czynniki, możesz przeprowadzić rozkład na czynniki pierwsze. Oznacza to, że szukasz liczb, które składają się na twój mianownik. W przypadku liczby 3 czynniki to 3 i 1. W przypadku liczby 4 czynniki to 2 i 2. W takim razie wszyscy. 3 x 2 x 2 = 12. Twój najmniejszy wspólny mianownik!
Pomnóż wszystkie liczby przez mniejszą liczbę. W niektórych problemach, takich jak ten, możesz pomnożyć obie liczby - 3 x 4 = 12. Jeśli jednak masz duży mianownik, nie rób tego! Nie chcesz pomnożyć 56 x 44 i iść na całość, aby uzyskać 2464

Krok 2. Pomnóż mianownik przez liczbę potrzebną do uzyskania najmniejszego wspólnego mianownika
Innymi słowy, chcesz, aby wszystkie twoje mianowniki były równe. W naszym przykładzie chcemy, aby mianownik wynosił 12. Aby zmienić 3 na 12, pomnóż 3 przez 4. Aby zmienić 4 na 12, pomnóż 4 przez 3. Ten sam mianownik będzie mianownikiem Twojej ostatecznej odpowiedzi.
-
Czyli 2/3 staje się 2/3 x 4, a 3/4 staje się 3/4 x 3. Oznacza to, że mamy teraz 2/12 i 3/12. Ale jeszcze nie skończyliśmy!
- Zauważysz, że mianowniki są mnożone przez siebie. Można to zrobić w tej sytuacji, ale nie we wszystkich sytuacjach. Czasami zamiast mnożyć oba mianowniki, można pomnożyć oba mianowniki przez inną liczbę, aby uzyskać mniejszą liczbę.
- W innych zadaniach czasami wystarczy pomnożyć jeden mianownik, aby był równy mianownikowi drugiego ułamka w zadaniu.

Krok 3. Pomnóż licznik przez tę samą liczbę
Kiedy mnożysz mianownik przez liczbę, musisz również pomnożyć licznik przez tę samą liczbę. To, co zrobiliśmy w ostatnim kroku, jest tylko częścią mnożenia, które należy wykonać.
W pierwszym kroku mamy 2/3x4 i 2/4x3 - potem w drugim kroku 2 x 4/3 x 4 i 3 x 3/4 x 3. Czyli nasze nowe liczby to 8/12 i 9/ 12. Doskonały
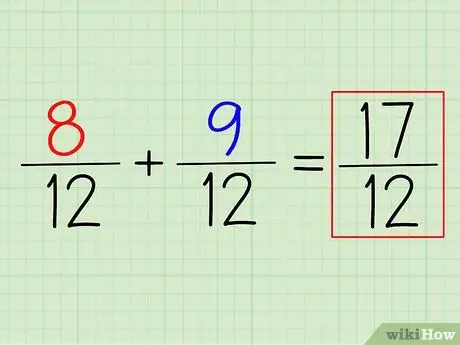
Krok 4. Dodaj (lub odejmij) liczniki, aby uzyskać odpowiedź
Aby dodać 8/12 + 9/12, wystarczy dodać liczniki. Pamiętaj: po prostu zostaw mianownik. Najmniejszy wspólny mianownik, jaki znajdziesz, to Twój ostateczny mianownik.
W tym przykładzie (8+9)/12 = 17/12. Aby zamienić ją na liczbę mieszaną, po prostu odejmij mianownik od licznika i zapisz resztę. W tym przypadku 17/12 = 15/12
Metoda 3 z 4: Dodawanie i odejmowanie ułamków mieszanych i wspólnych
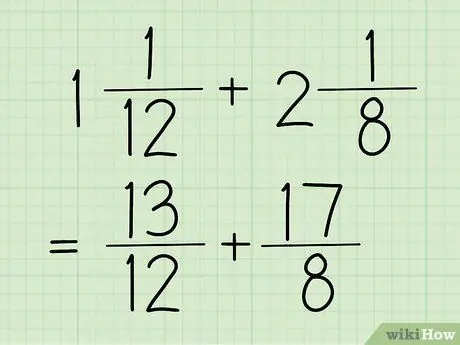
Krok 1. Konwertuj ułamki mieszane na zwykłe ułamki
Liczba mieszana to ułamek, który ma liczbę całkowitą i ułamek, jak w powyższym przykładzie (1 5/12). Tymczasem zwykły ułamek to taki, którego licznik (liczba górna) jest większy od mianownika (liczba dolna). Ta frakcja jest również widoczna w poprzednim kroku, czyli 17/12.
W przykładach w tej sekcji użyjemy 13/12 i 17/8

Krok 2. Znajdź wspólny mianownik
Czy pamiętasz trzy sposoby na znalezienie najmniejszego wspólnego mianownika? Pisząc wielokrotności, stosując rozkład na czynniki pierwsze lub mnożąc mianowniki.
Znajdźmy wielokrotności naszego przykładu, 12 i 8. Jaka jest najmniejsza liczba, którą mają ze sobą wspólnego? 24. 8, 16, 24 i 12, 24 - bingo

Krok 3. Pomnóż swój licznik i mianownik, aby znaleźć równoważny ułamek
Oba mianowniki należy zmienić na 24. Jak przeliczyć 12 na 24? Pomnóż przez 2,8 do 24? Pomnóż przez trzy. Ale nie zapomnij - liczniki też trzeba pomnożyć!
Tak więc (13 x 2)/(12 x 2) = 26/24. I (17 x 3)/(8 x 3) = 51/24. Prawie z tym skończyliśmy

Krok 4. Dodaj lub odejmij swoje ułamki
Teraz, gdy masz ten sam mianownik, możesz łatwo dodać oba liczniki razem. Pamiętaj, po prostu zostaw mianownik!
26/24 + 51/24 = 77/24. To twoja suma! Jednak liczby na górze były zbyt duże…

Krok 5. Konwertuj swoją odpowiedź z powrotem na liczby mieszane
Bardzo duża liczba na górze ułamka wydaje się nieco dziwna - nie możesz określić rozmiaru swojego ułamka. Wszystko, co musisz zrobić, to kilkakrotnie odjąć swój mianownik od licznika, aż nie będzie można go dalej odjąć, i zapisać resztę.
-
W tym przykładzie 77 odjąć 24 3 razy. To znaczy 24 x 3 = 72. Reszta to 5! Jaki jest Twój wynik końcowy? 3 5/24.
Tak prawdziwe!
Metoda 4 z 4: Dodawanie i odejmowanie ułamków bez znajdowania LCM
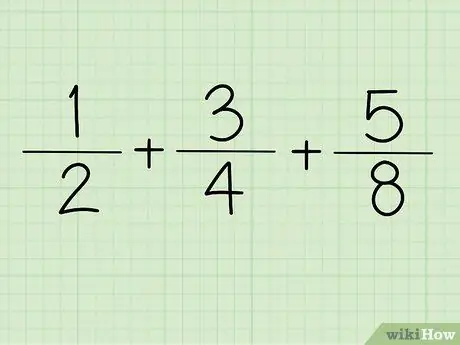
Krok 1. Zapisz ułamek
Na przykład + +

Krok 2. Najpierw rozwiąż licznik
- Pomnóż przez licznik drugiej frakcji.
- Pomnóż 1 przez 4 i 8. [32]
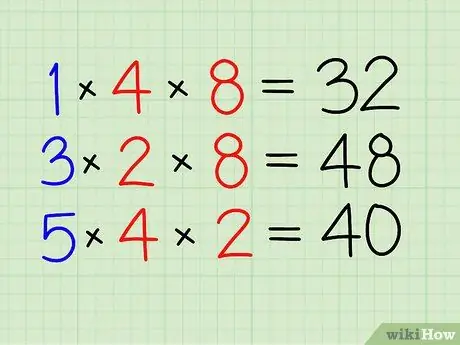
Krok 3. Zrób to samo dla pozostałych frakcji
- Pomnóż 3 przez 2 i 8. [48]
- Na koniec pomnóż 5 przez 4 i 2. [40]
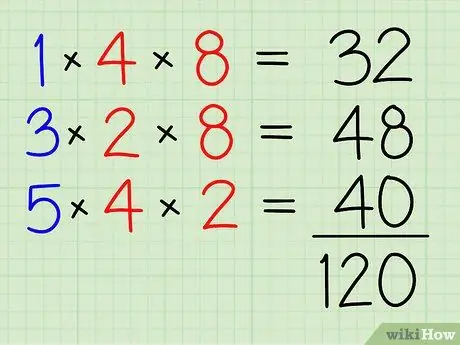
Krok 4. Dodaj je wszystkie razem
32+48+40=120
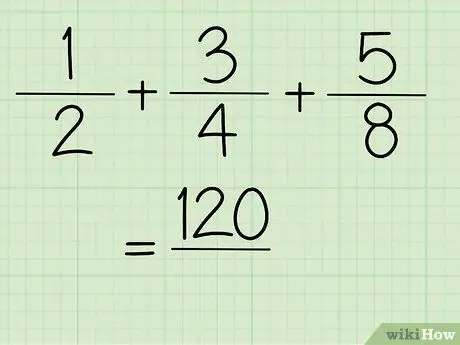
Krok 5. Teraz otrzymujesz wartość licznika

Krok 6. Rozwiąż mianownik ułamka

Krok 7. Pomnóż wszystkie mianowniki ułamków
2×4×8=64

Krok 8. Teraz otrzymujesz wynik
120/64 = 1 56/64 = 1 ⅞
Ostrzeżenie
- Ta metoda pozwala mnożyć duże liczby.
- Do obliczenia w ten sposób możesz potrzebować kalkulatora.






