- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:21.
- Ostatnio zmodyfikowany 2025-06-01 06:07.
Możesz pomyśleć, że liczby całkowite to zwykłe liczby, takie jak 3, -12, 17, 0, 7000 lub -582. Liczby całkowite są również nazywane liczbami całkowitymi, ponieważ nie są dzielone na części, takie jak ułamki zwykłe i dziesiętne. Przeczytaj ten artykuł, aby dowiedzieć się wszystkiego, czego potrzebujesz na temat dodawania i odejmowania liczb całkowitych, lub przeczytaj bezpośrednio odpowiednią sekcję.
Krok
Metoda 1 z 5: Dodawanie i odejmowanie dodatnich liczb całkowitych za pomocą linii liczbowej

Krok 1. Zapoznaj się z linią liczbową
Linie liczbowe zmieniają podstawową matematykę w coś namacalnego i fizycznego, co możesz zobaczyć. Za pomocą kilku znaków i zdrowego rozsądku możemy używać go jak kalkulatora do dodawania i odejmowania liczb.

Krok 2. Narysuj podstawową linię liczbową
Wyobraź sobie lub narysuj równą linię prostą. Zrób kropkę na środku linii. Pisać 0 lub zero obok tego okresu.
Twoja książka do matematyki może nazwać to punktem wyjścia, ponieważ jest to punkt wyjścia dla wszystkich liczb

Krok 3. Narysuj dwie kropki, po jednej na prawo i lewo od zera
Pisać - 1 obok kropki po lewej i
Krok 1. obok kropki po prawej stronie. Jest to liczba całkowita najbliższa zeru.
- Nie martw się, że odległości między punktami będą dokładnie takie same - jeśli wiesz, co oznacza każdy punkt, możesz użyć osi liczbowej.
- Lewa strona to początek zdania.

Krok 4. Uzupełnij linię liczbową, dodając więcej liczb
Zrób więcej kropek po lewej niż -1 i po prawej niż 1. Po lewej stronie, od -1, zaznacz kropki - 2, - 3, oraz - 4. Po prawej stronie, od 1, zaznacz swoją kropkę
Krok 2
Krok 3., da
Krok 4.. Możesz kontynuować, jeśli masz miejsce na papierze.
Przykład na rysunku pokazuje linię liczbową od -6 do 6

Krok 5. Zapoznaj się z liczbami całkowitymi dodatnimi i ujemnymi
Liczby całkowite dodatnie, zwane również Liczba naturalna, jest liczbą całkowitą większą od zera. 1, 2, 3, 25, 99 i 2007 są liczbami całkowitymi dodatnimi. Ujemne liczby całkowite to liczby całkowite mniejsze od zera (takie jak -2, -4 i -88).
Liczby całkowite to kolejny sposób na wywoływanie liczb całkowitych. Ułamki takie jak 1/2 (połowa) są tylko częścią liczby, więc nie są liczbami całkowitymi. To samo, co dziesiętne, na przykład 0,25 (przecinek zero dwa pięć); dziesiętny nie jest liczbą całkowitą

Krok 6. Rozpocznij rozwiązywanie 1+2, umieszczając palec na punkcie 1
Rozwiążemy proste problemy z dodawaniem 1+2 używając właśnie utworzonej linii liczbowej. Pierwsza liczba to
Krok 1., więc zacznij kłaść palec na numerze.
-
Czy to pytanie jest zbyt proste?
Jeśli kiedykolwiek dodałeś, prawdopodobnie znasz odpowiedź na 1+2. Dobrze: jeśli znasz wynik, łatwiej będzie zrozumieć, jak działa oś liczbowa. Następnie możesz użyć osi liczbowej, aby rozwiązać trudniejsze zadania z dodawaniem lub przygotować się do trudniejszej matematyki, takiej jak algebra.

Krok 7. Dodaj 1+2, przesuwając palcem o 2 kropki w prawo
Przesuń palec w prawo, licząc liczbę kropek (inną liczbę), które mijasz. Jeśli zdałeś 2 nowe punkty, zatrzymaj się. Liczba, na którą wskazuje twój palec, jest odpowiedzią,
Krok 3
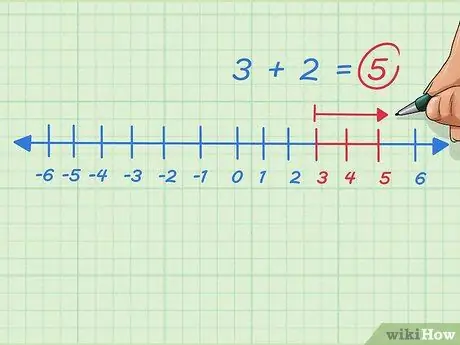
Krok 8. Dodaj dowolne dodatnie liczby całkowite, przesuwając się w prawo na osi liczbowej
Załóżmy, że chcemy rozwiązać 3+2. Zacznij od 3, przejdź w prawo lub dodaj 2 kropki. Zatrzymujemy się na 5. Problem jest napisany 3 + 2 = 5.

Krok 9. Odejmij dodatnie liczby całkowite, przesuwając się w lewo na osi liczbowej
Na przykład, chcemy rozwiązać 6 -4, zaczynamy od 6, przesuwamy się w lewo o 4 punkty i kończymy na 2. Ten problem jest napisany 6 - 4 = 2.
Metoda 2 z 5: Dodawanie i odejmowanie liczb ujemnych za pomocą linii liczbowej

Krok 1. Dowiedz się o liniach liczbowych
Jeśli nie wiesz, jak utworzyć oś liczbową, wróć do sekcji Dodawanie i odejmowanie liczb dodatnich za pomocą osi liczbowych, aby dowiedzieć się, jak utworzyć oś liczbową.
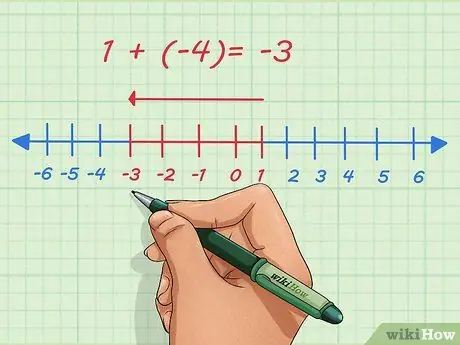
Krok 2. Zrozum o liczbach ujemnych
Liczby dodatnie są oznaczone kierunkiem w prawo na osi liczbowej. Liczby ujemne są wskazane po lewej stronie na osi liczbowej. Dodanie liczb ujemnych oznacza przesunięcie punktu w lewo na osi liczbowej.
-
Na przykład dodajmy 1 i -4. Zwykle to pytanie jest napisane tak:
1 + (-4)
. Na osi liczbowej zaczynamy od 1, przesuwamy o 4 punkty w lewo i zatrzymujemy się na -3.
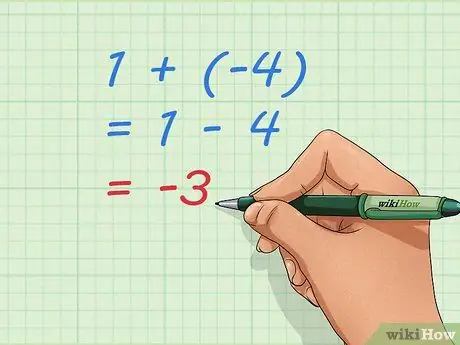
Krok 3. Użyj podstawowych równań, aby zrozumieć dodawanie liczb ujemnych
Zauważ, że -3, nasza odpowiedź, to liczba, którą otrzymamy, jeśli zrobimy 1 - 4. Dodanie 1 + (-4) i odjęcie 4 od 1 to ten sam problem. Możemy zapisać to jako równanie, zdanie matematyczne, które pokazuje równość:1 + (-4) = 1-4 = -3
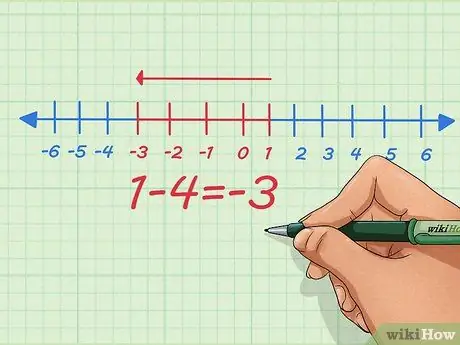
Krok 4. Zamiast dodawać liczby ujemne, zamień je w problem odejmowania za pomocą liczb dodatnich
Jak widać z prostego równania powyżej, możemy zrobić jedno i drugie - zamienić dodawanie liczb ujemnych na odejmowanie liczb dodatnich i odwrotnie. Być może nauczono cię zamieniać negatywy w negatywy, nie wiedząc dlaczego - oto dlaczego.
-
Na przykład -4. Kiedy dodamy -4 i 1, odejmiemy 1 przez 4. Można to zapisać matematycznie pisząc
1 + (-4) = 1 - 4
. Możemy to zapisać na osi liczbowej, zaczynając od naszego punktu początkowego od 1, a następnie dodając 4 kropki z lewej strony (innymi słowy, dodając -4). Ponieważ to jest równanie, jedno jest równe drugiemu - więc odwrotnie też jest prawdziwe
1 - 4 = 1 + (-4)
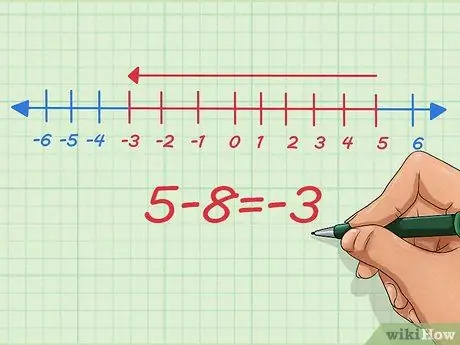
Krok 5. Dowiedz się, jak odjąć liczby ujemne na osi liczbowej
Na osi liczbowej odejmowanie liczb ujemnych jest tym samym, co zmniejszanie długości. Zacznijmy od 5 - 8.
Na osi liczbowej zaczynamy od punktu początkowego 5, odejmujemy 8 i zatrzymujemy się na -3
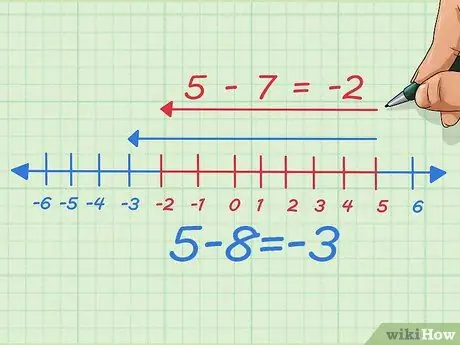
Krok 6. Odejmij kwotę, którą odejmujesz i zobacz, co się stanie
Załóżmy, że odejmiemy jeden, liczbę, którą odejmiemy, lub innymi słowy odejmiemy 7 zamiast 8. Teraz odejmujemy jeden punkt w lewo na osi liczbowej. Na piśmie zaczęliśmy od 5 - 8 = -3 Teraz po prostu przesuwamy 7 w lewo, więc staje się 5 - 7 = -2
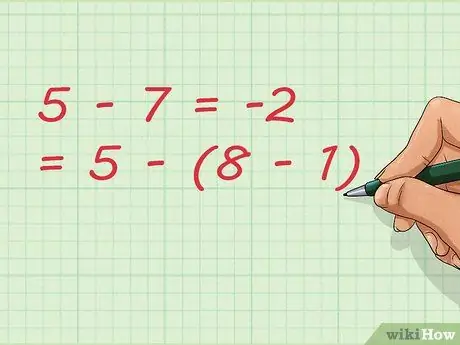
Krok 7. Zauważ, że odejmowanie może skutkować dodawaniem
W naszym przykładzie odejmujemy liczbę 1. Pisząc równanie, możemy zapisać je krócej: 5 - 7 = -2 = 5 - (8 - 1)

Krok 8. Konwertuj znaki ujemne na dodatnie podczas dodawania liczb ujemnych
Korzystając z kroku konwersji wszystkich odejmowań na dodawania, możemy napisać krótsze odejmowania, takie jak: 5 - (8 - 1) = 5 - 7 = 5 - 8 + 1.
-
Wiemy już, że 5 - 8 = -3, więc weź 5 - 8 z równania i wpisz -3:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
Wiemy już, że 5 - (8 - 1) to - odejmuje jeden punkt od 5 - 8. Nasze równanie może pokazać, że 5 - 8 równa się -3, a odjęcie jednego punktu daje -2. Równanie można zapisać w następujący sposób:
-3 - (-1) = -3 + 1
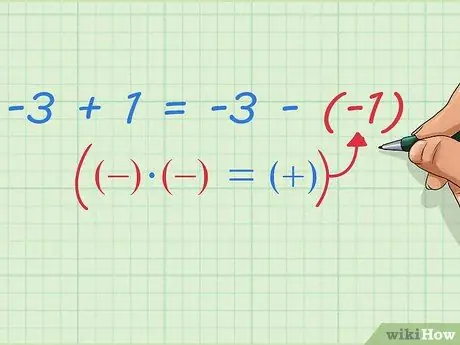
Krok 9. Zapisz odejmowanie liczb ujemnych jako dodawanie
Zwróć uwagę, co dzieje się po tym - już udowodniliśmy, że: -3 + 1 = -3 - (-1) Możemy to napisać za pomocą prostszych i bardziej ogólnych zasad matematycznych: pierwsza liczba plus druga liczba = pierwsza liczba minus (druga liczba ujemna) Lub prostszy sposób, który prawdopodobnie słyszałeś na lekcji matematyki: Zmień dwa znaki ujemne na znak dodatni.
Metoda 3 z 5: Dodawanie dodatnich dużych liczb całkowitych

Krok 1. Napisz zadanie dodawania 2503 + 7461 z jedną liczbą nad drugą
Zapisz liczby w dużej kolumnie tak, że 2 jest ponad 7, 5 jest ponad 4 i tak dalej. W ten sposób nauczymy się dodawać liczby całkowite, które są zbyt duże, aby sobie wyobrazić lub wykorzystać oś liczbową.
Napisz znak + po lewej stronie liczby poniżej i linii pod nim, jak możesz się nauczyć w przypadku mniejszych problemów z dodawaniem
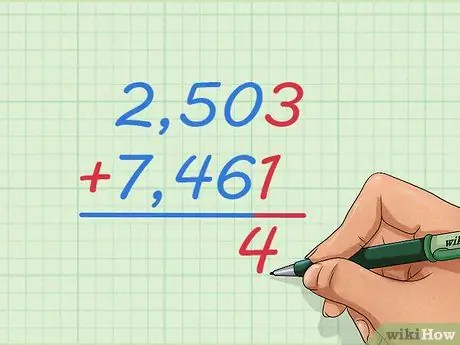
Krok 2. Zacznij od dodania dwóch liczb po prawej stronie
Może być trochę dziwnie zacząć od prawej, ponieważ odczytujemy liczby od lewej. Musimy dodać od prawej, aby uzyskać poprawną odpowiedź, którą możesz zobaczyć później.
-
Pod dwiema skrajnymi liczbami po prawej stronie
Krok 3. da
Krok 1., zapisz sumę tych dwóch
Krok 4..

Krok 3. Dodaj każdą liczbę w kolumnie w ten sam sposób
Przesuń się w lewo, zsumuj 0+6, 5+4, oraz 2+7. Napisz odpowiedź pod każdą parą cyfr.
Twoja odpowiedź powinna brzmieć: 9.964. Sprawdź swoją pracę, jeśli się pomylisz.

Krok 4. Teraz dodaj 857+135
Zauważysz coś innego, gdy tylko dodasz pierwszą parę liczb po prawej stronie. 7+5 równa się 12, liczba dwucyfrowa, ale pod tą kolumną możesz wpisać tylko jedną cyfrę. Czytaj dalej, aby dowiedzieć się, co powinieneś zrobić i dlaczego zawsze powinieneś zaczynać od prawej, a nie od lewej.

Krok 5. Dodaj 7+5 i dowiedz się, gdzie napisać odpowiedź
7+5=12, ale nie możesz umieścić 1 i 2 pod linią. Ale zapisz ostatnią cyfrę, Krok 2., pod linią i zapisz pierwszą cyfrę
Krok 1., nad kolumną po lewej stronie, 5+3.
-
Jeśli ciekawi Cię, jak to działa, zastanów się, co oznacza dzielenie 1 i 2. W rzeczywistości dzielisz 12 na
Krok 10. da
Krok 2.. Możesz napisać 10 nad liczbą, jeśli chcesz, a zobaczysz 1 w kolumnach 5 i 3, tak jak poprzednio.

Krok 6. Dodaj 1+5+3, aby otrzymać następną cyfrę odpowiedzi
Teraz masz trzy cyfry do zsumowania, ponieważ dodałeś 1 do tej kolumny. Odpowiedź to
Krok 9., więc twoja odpowiedź brzmi 92.
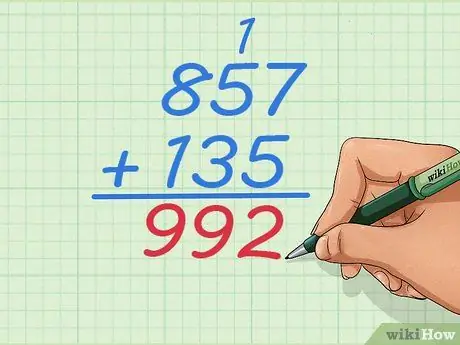
Krok 7. Rozwiąż problem jak zwykle
Kontynuuj pracę nad cyframi po lewej stronie, aż zsumujesz wszystkie liczby, w tym przypadku pozostała tylko jedna kolumna. Twoja ostateczna odpowiedź powinna brzmieć 992.
- Możesz spróbować bardziej skomplikowanych pytań, takich jak 974+568. Pamiętaj, że za każdym razem, gdy otrzymasz dwucyfrowy numer, wpisz tylko ostatnią cyfrę jako odpowiedź i umieść drugą cyfrę nad kolumną po lewej stronie, którą dodasz w następnej kolejności. Jeśli odpowiedź w ostatniej kolumnie (z lewej strony) zawiera dwie cyfry, zapisz ją jako swoją odpowiedź.
- Zobacz sekcję Porady, aby uzyskać odpowiedzi na pytania 974+568, gdy już spróbujesz je rozwiązać.
Metoda 4 z 5: Odejmowanie dodatnich dużych liczb całkowitych

Krok 1. Napisz zadanie odejmowania 4.713 - 502 z pierwszą liczbą powyżej drugiej
Napisz to tak, że 3 jest bezpośrednio nad 2, 1 jest nad 0, 7 jest nad 5, a 4 jest nad pustym polem.
Możesz wpisać 0 pod 4, jeśli to pomoże Ci zapamiętać, która liczba jest powyżej której. Zawsze możesz dodać 0 przed liczbą bez jej zmiany. Pamiętaj, aby dodać go przed numerem, a nie po nim

Krok 2. Odejmij każdą liczbę poniżej od liczby bezpośrednio nad nią
Zawsze zaczynaj od prawej. Rozwiąż 3-2, 1-0, 7-5 i 4-0, napisz odpowiedź na każde pytanie bezpośrednio pod dwiema odjętymi liczbami.
Wynik to, 4.211.

Krok 3. Teraz w ten sam sposób napisz pytania 924 - 518
Liczby te mają taką samą liczbę cyfr, dzięki czemu można je łatwo zapisać. Ten problem nauczy Cię czegoś o odejmowaniu liczb całkowitych, jeśli jeszcze go nie znasz.

Krok 4. Dowiedz się, jak rozwiązać pierwszy problem, który znajduje się po prawej stronie
4 - 8. Ten problem jest skomplikowany, ponieważ 4 jest mniejsze niż 8, ale nie używaj liczb ujemnych, ale wykonaj następujące kroki:
- W górnym rzędzie przekreśl 2 i napisz 1. 2 powinno znajdować się na lewo od 4.
- Przekreśl 4 i napisz 14. Zrób to w wąskim miejscu, aby było jasne, że 14 to ponad 8. Możesz również napisać 1 przed 4, aby uzyskać 14, jeśli jest wystarczająco dużo miejsca.
- To, co właśnie zrobiłeś, to pożyczenie 1 z miejsca dziesiątek lub drugiej kolumny od prawej i przekonwertowanie na 10 w miejscu jedynek lub skrajnej prawej kolumnie. Gdy liczba 10 jest równa dziesięciokrotności liczby 1, to jest to samo.

Krok 5. Teraz rozwiąż zadania 14 - 8 i napisz odpowiedź pod skrajną prawą kolumną
Powinno być napisane 6 w skrajnej prawej linii odpowiedzi.

Krok 6. Uzupełnij następną kolumnę po lewej stronie, używając nowego zapisanego numeru
Odejmowanie powinno wynosić 1 - 1, co jest równe 0.
Twoja odpowiedź powinna teraz brzmieć 06.

Krok 7. Rozwiąż problem, wykonując ostatnie odejmowanie, skrajną lewą kolumnę
9 - 5 = 4, więc Twoja ostateczna odpowiedź to 406.

Krok 8. Teraz rozwiązujemy problem odejmowania dużych liczb od małych
Załóżmy, że zostaniesz poproszony o wypełnienie 415.990 - 968.772. Wpisz drugą liczbę pod pierwszą, a zdasz sobie sprawę, że liczba poniżej jest większa! Możesz od razu rozpoznać po pierwszej cyfrze po lewej: 9 jest większe niż 4, więc liczby zaczynające się od 9 są większe.
Upewnij się, że zapisałeś kolumnę poprawnie przed porównaniem. 912 nie większe niż 5000 możesz stwierdzić, czy wpisujesz kolumnę poprawnie, ponieważ nie ma liczb poniżej 5. Możesz dodać zero pomocy, na przykład wpisz 912 z 0912, aby kolumna była równa 5000.

Krok 9. Wpisz mniejszą liczbę pod większą liczbą i dodaj znak - przed odpowiedzią
Za każdym razem, gdy odejmujesz liczbę od mniejszej liczby, wynikiem jest liczba ujemna. Lepiej napisać ten znak przed odjęciem, aby nie zapomnieć go zapisać.

Krok 10. Aby odpowiedzieć, odejmij małą liczbę od dużej i pamiętaj, aby wpisać znak -
Twoja odpowiedź będzie negatywna, na co wskazuje znak -. Nie rób próbuje odjąć dużą liczbę od małej, a następnie daje wynik ujemny; twoja odpowiedź będzie błędna.
Nowy problem do rozwiązania to: 968 772 - 415 990 = -? Zobacz sekcję Wskazówki, aby uzyskać odpowiedź po próbie rozwiązania tego problemu
Metoda 5 z 5: Dodawanie i odejmowanie ujemnych liczb całkowitych
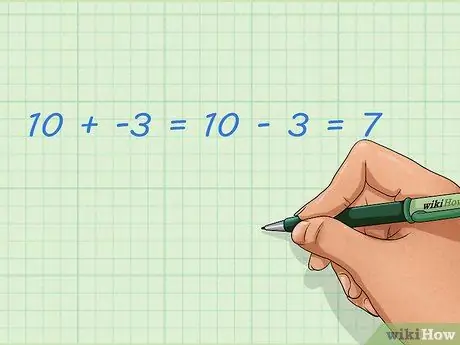
Krok 1. Dowiedz się, jak dodawać liczby ujemne i dodatnie
Dodawanie ujemnych liczb całkowitych jest takie samo jak odejmowanie dodatnich liczb całkowitych. Łatwiej to zrobić z osią liczbową opisaną w innej sekcji, ale możesz też o tym myśleć słowami. Liczby ujemne nie są zwykłymi liczbami; ta liczba jest mniejsza od zera i może reprezentować pobraną kwotę. Jeśli dodasz to dubel do zwykłej liczby, wynik będzie mniejszy.
- Przykład: 10 + -3 = 10 - 3 = 7
- Przykład: -12 + 18 = 18 + -12 = 18 - 12 = 6. Pamiętaj, że zawsze możesz zmienić kolejność liczb dodając, ale nie odejmując.
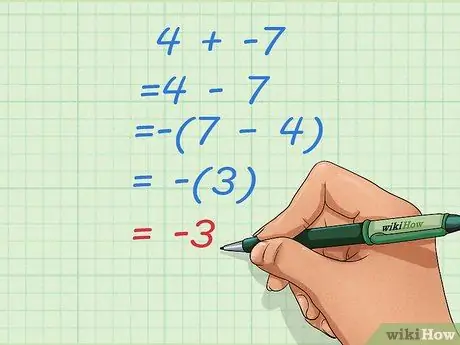
Krok 2. Dowiedz się, co musisz zrobić, jeśli zamienisz to w problem odejmowania z mniejszą liczbą początkową
Czasami zmiana dodawania do problemów z odejmowaniem, takich jak ten powyżej, może prowadzić do nieparzystych odpowiedzi, takich jak 4-7. Kiedy tak się stanie, odwróć kolejność liczb i spraw, aby wynik był ujemny.
- Powiedzmy, że twój początkowy problem to 4 + -7.
- Zamień to w problem odejmowania: 4 - 7
- Odwróć kolejność i ustaw wynik ujemny: -(7 - 4) = -(3) = -3.
- Jeśli nie jesteś zaznajomiony z używaniem nawiasów w równaniach, pomyśl o tym: 4 - 7 zamienia się w 7 - 4 z dodatkiem znaku ujemnego. 7 - 4 = 3, ale musimy zmienić to na -3, aby odpowiedź na pytania 4 - 7 była prawidłowa.
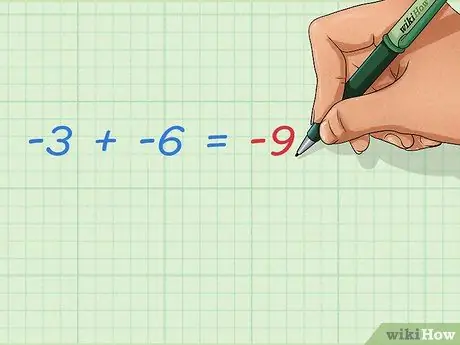
Krok 3. Dowiedz się, jak dodać dwie ujemne liczby całkowite
Dodanie dwóch liczb ujemnych zawsze zwiększa ujemny wynik. Ponieważ nie są dodawane żadne liczby dodatnie, wynik będzie dalej od zera. Odpowiedź jest prosta:
- -3 + -6 = -9
- -15 + -5 = -20
- Czy widzisz wzór? Wszystko, co musisz zrobić, to zsumować liczby tak, jakby były liczbami dodatnimi i dodać znak ujemny. -4 + -3 = -(4 + 3) = -7
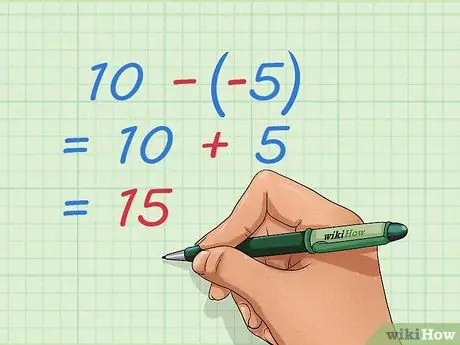
Krok 4. Naucz się odejmować ujemne liczby całkowite
Podobnie jak problem dodawania, możesz przepisać problem, aby mieć tylko liczby dodatnie. Odejmując liczby ujemne, usuwasz niektóre rzeczy, które już zostały zabrane, co jest równoznaczne z dodawaniem liczb dodatnich.
- Pomyśl o liczbach ujemnych jak o skradzionych pieniądzach. Jeśli odejmiesz lub zabierzesz skradzione pieniądze, aby móc je zwrócić, to tak, jakbyś komuś dał pieniądze, prawda?
- Przykład: 10 - -5 = 10 + 5 = 15
- Przykład: -1 - -2 = -1 + 2. Nauczyłeś się już, jak rozwiązać ten problem w pierwszym kroku, pamiętasz? Przeczytaj ponownie, jak dodawać liczby ujemne i dodatnie, jeśli zapomniałeś.
- Oto kompletne rozwiązanie ostatniego przykładu: -1 - -2 = -1 + 2 = 2 + -1 = 2 - 1 = 1.
Porady
- Być może wpisałeś długie liczby, takie jak 2 521 301, używając przecinków (,) zamiast (.) w zależności od miejsca zamieszkania. Użyj tego, o co prosi twój nauczyciel, aby nie pomylić się z innymi systemami pisma.
- Narysuj swoje linie liczbowe na różnych skalach, aby reprezentować różne liczby. Nie ma reguły, że każda odległość na osi liczbowej równa się 1. Wyobraź sobie oś liczbową, która ma 10 zamiast 1. Oprócz tego, że każdy punkt ma teraz 10, dodawanie i odejmowanie pozostają takie same. Spróbuj, jeśli w to nie wierzysz.
- Jeśli wypróbujesz specjalne pytania testowe w sekcji Długie liczby, oto odpowiedź: 974 + 568 = 1.542. Odpowiedź od 415 990 - 968 772 to - 552.782.






