- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:13.
- Ostatnio zmodyfikowany 2025-06-01 06:07.
Odejmowanie to po prostu odejmowanie jednej liczby od drugiej. Łatwo jest odjąć jedną liczbę całkowitą od drugiej, ale odejmowanie może być trudne, jeśli odejmujesz ułamki zwykłe lub dziesiętne. Gdy zrozumiesz odejmowanie, będziesz w stanie używać bardziej złożonych pojęć matematycznych i łatwiej dodawać, mnożyć i dzielić liczby.
Krok
Metoda 1 z 6: Odejmowanie dużych liczb całkowitych przez pożyczanie

Krok 1. Zapisz dużą liczbę
Na przykład chcesz rozwiązać 32 - 17. Najpierw zapisz 32.

Krok 2. Wpisz mniejszą liczbę tuż pod nią
Upewnij się, że umieściłeś wartości dziesiątek i jedynek w odpowiednich kolumnach, tak aby 3 z 32 znajdowało się bezpośrednio nad 1 z 17, a 2 z 32 było bezpośrednio nad 7 z 17.
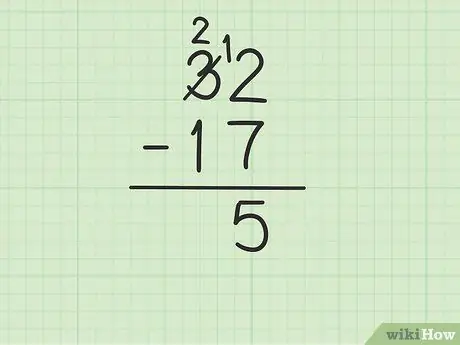
Krok 3. Odejmij górną liczbę w kolumnie jednostek od liczby na dole
Jednak może się to skomplikować, jeśli dolna liczba jest większa niż górna liczba. W tym przypadku 7 jest większe niż 2. Oto, co musisz zrobić:
- Musisz pożyczyć z liczby 3 z 32 (znanej również jako grupowanie), aby zmienić 2 w 12.
- Przekreśl cyfrę 3 z 32 i zastąp ją cyfrą 2, podczas gdy cyfra 2 stanie się 12.
- Teraz możesz odjąć 12 - 7, co daje 5. Wpisz 5 pod dwiema liczbami, które odejmujesz, tak aby znajdowały się w kolumnie jednostek nowego wiersza.
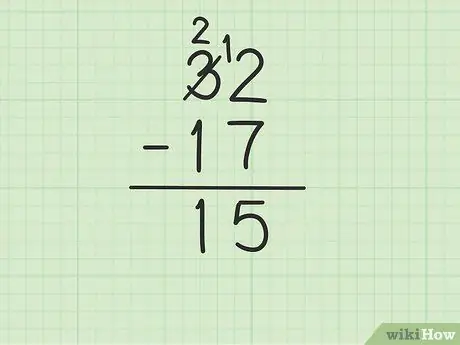
Krok 4. Odejmij górną liczbę w kolumnie dziesiątek od dolnej liczby
Pamiętaj, że 3 stało się 2. Teraz odejmij 1 od 17 od 2 powyżej, aby otrzymać (2-1) 1. Wpisz 1 poniżej, w kolumnie dziesiątek, na lewo od 5 w kolumnie jednostek. Piszesz 15. To znaczy 32 - 17 = 15.
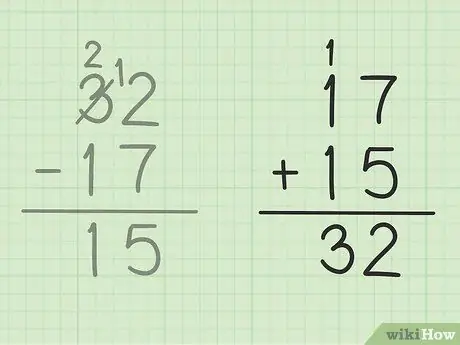
Krok 5. Sprawdź swoją pracę
Jeśli chcesz się upewnić, że poprawnie odjąłeś dwie liczby, wszystko, co musisz zrobić, to zsumować swoją odpowiedź z mniejszą liczbą, aby uzyskać dużą liczbę. W tym zadaniu musisz dodać swoją odpowiedź, 15 do mniejszej liczby odejmowania, 17. 15 + 17 = 32, aby Twoja odpowiedź była poprawna. Bezpieczna!
Metoda 2 z 6: Odejmij małe liczby całkowite
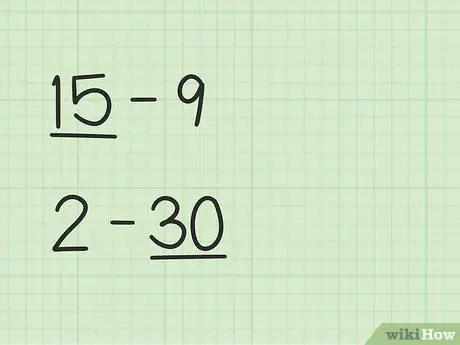
Krok 1. Znajdź większą liczbę
Problemy typu 15 -9 będą miały inny sposób niż 2 - 30.
- W pytaniach 15 - 9 pierwsza liczba, 15, jest większa od drugiej liczby, 9.
- W pytaniach 2 - 30 druga liczba, 30, jest większa niż pierwsza liczba, 2.
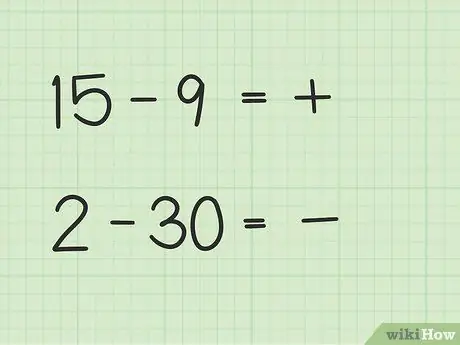
Krok 2. Zdecyduj, czy Twoja odpowiedź będzie pozytywna czy negatywna
Jeśli pierwsza liczba jest większa, odpowiedź jest pozytywna. Jeśli druga liczba jest większa, odpowiedź jest negatywna.
- W pierwszym pytaniu 15-9 Twoja odpowiedź jest pozytywna, ponieważ pierwsza liczba jest większa od drugiej.
- W drugim pytaniu, 2 - 30, twoja odpowiedź jest negatywna, ponieważ druga liczba jest większa od pierwszej.
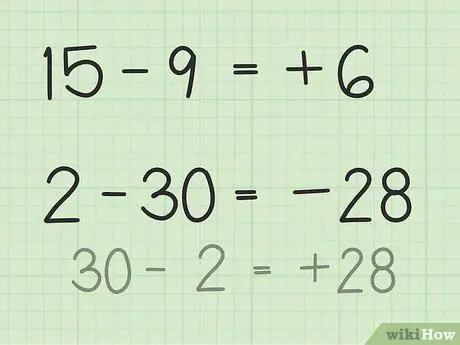
Krok 3. Znajdź różnicę między dwiema liczbami
Aby odjąć dwie liczby, musisz wyobrazić sobie różnicę między tymi dwiema liczbami i obliczyć liczby między nimi.
- W przypadku pytań 15 - 9 wyobraź sobie stos 15 żetonów pokerowych. Wyrzuć 9 żetonów i tylko 6. Tak więc 15 - 9 = 6. Możesz również wyobrazić sobie linię liczbową. Pomyśl o liczbach od 1 do 15, a następnie odrzuć lub zwróć 9 jednostek, aby otrzymać 6.
- W przypadku pytań 2 - 30 najłatwiejszym sposobem rozwiązania tego problemu jest odwrócenie liczby i po odjęciu ujemnego wyniku. Zatem 30 - 2 = 28, więc 28 i 30 mają różnicę 2. Teraz zrób wynik ujemny, ponieważ już ustaliłeś, że odpowiedź jest ujemna, ponieważ druga liczba jest większa od pierwszej. Tak więc 2 - 30 = -28.
Metoda 3 z 6: Odejmowanie ułamków dziesiętnych
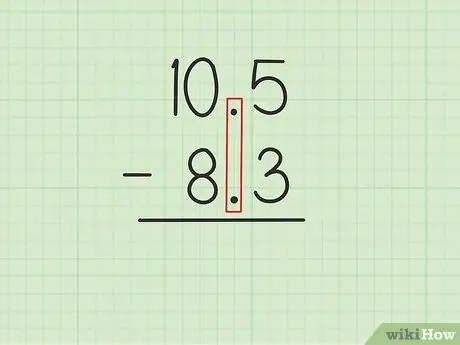
Krok 1. Napisz większą liczbę nad mniejszą liczbą z wyrównanymi kropkami dziesiętnymi
Załóżmy, że chcesz rozwiązać następujące problemy: 10, 5 - 8, 3. Zapisz 10, 5 przez 8, 3 tak, aby miejsca dziesiętne dwóch liczb były równoległe., 5 z 10, 5 musi znajdować się bezpośrednio powyżej, 3 z 8, 3 i 0 z 10, 5 musi znajdować się powyżej 8 z 8, 3.
Jeśli masz problem, ponieważ dwie liczby nie mają tej samej liczby po przecinku, wpisz 0 w puste miejsce, aż suma liczb będzie taka sama. Na przykład problem to 5, 32 - 4, 2, możesz zapisać to jako 5, 32 - 4, 2 0. Nie zmieni to wartości drugiej liczby, ale ułatwi odejmowanie tych dwóch liczb.

Krok 2. Odejmij najwyższą liczbę w kolumnie dziesiątek od liczby poniżej
W tym przypadku musisz odjąć 3 od 5. 5 - 3 = 2, więc musisz zapisać 2 pod 3 z 8, 3.
Upewnij się, że w odpowiedzi umieściłeś kropkę dziesiętną, tak aby była napisana, 2

Krok 3. Odejmij liczbę nad kolumną jednostek od liczby pod nią
Musisz odjąć 8 od 0. Pożycz 1 od części dziesiątek, aby zmienić 0 na 10 i odejmij 10 - 8, aby uzyskać 2. Możesz też policzyć 10 - 8 bez pożyczania, ponieważ w drugiej kolumnie dziesiątek nie ma żadnych liczb. Napisz odpowiedź pod 8, na lewo od przecinka.

Krok 4. Zapisz swój wynik końcowy
Twój wynik końcowy to 2, 2.

Krok 5. Sprawdź swoją pracę
Jeśli chcesz się upewnić, że odejmowanie dziesiętne jest poprawne, wystarczy, że zsumujesz odpowiedź z mniejszą liczbą, aby uzyskać większą liczbę. 2, 2 + 8, 3 = 10, 5, więc skończyłeś.
Metoda 4 z 6: Odejmij ułamki

Krok 1. Wyrównaj mianownik i licznik ułamka
Załóżmy, że chcesz rozwiązać zadania 13.10 - 3.05. Napisz zadanie tak, aby dwa liczniki 13 i 3 oraz dwa mianowniki 10 i 5 były naprzeciw siebie. Te dwie liczby są oddzielone znakiem odejmowania. Pomoże to zwizualizować problem i łatwiej go rozwiązać.

Krok 2. Znajdź najmniej wspólny mianownik
Najmniejszy wspólny mianownik to najmniejsza liczba, którą można podzielić przez dwie liczby. W tym przykładzie musisz znaleźć najmniejszy wspólny mianownik, który jest podzielny przez 10 i 5. Zobaczysz, że 10 jest najmniejszym wspólnym mianownikiem dla obu liczb, ponieważ 10 jest podzielne przez 10 i 5.
Zauważ, że najmniejszym wspólnym mianownikiem dwóch liczb nie zawsze jest jedna z nich. Na przykład najmniejszym wspólnym mianownikiem 3 i 2 jest 6, ponieważ 6 to najmniejsza liczba, którą można podzielić przez dwie liczby
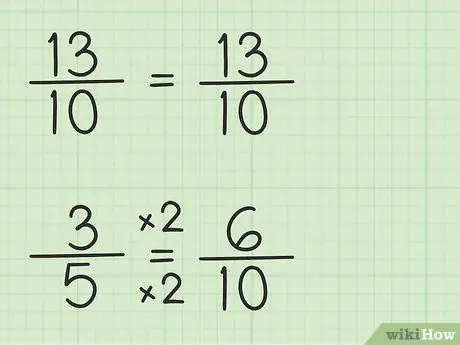
Krok 3. Zapisz ułamki, używając tego samego mianownika
Ułamek 13/10 można zapisać w ten sam sposób, ponieważ mianownik to 10, najmniejszy wspólny mianownik, czyli 10 razy 1. Jednak ułamek 3/5 musi zostać przepisany, ponieważ mianownik to 5, najmniejszy wspólny mianownik, czyli 10 razy 2. Zatem ułamek 3/5 musi zostać pomnożony przez 2/2, aby otrzymać mianownik 10, czyli 3/5 x 2/2 = 6/10. Znalazłeś równoważny ułamek. 3/5 odpowiada 6/10, chociaż 6/10 pozwala odjąć pierwszą liczbę, 13/10.
Napisz nowe pytanie w ten sposób: 13.10 - 6.10
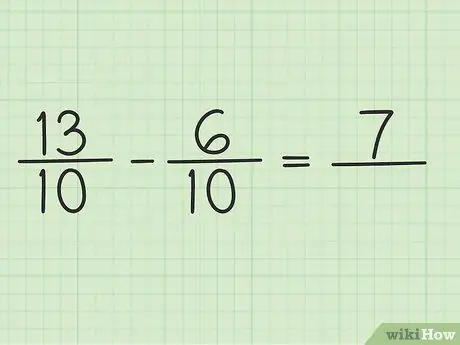
Krok 4. Odejmij licznik od dwóch liczb
Po prostu odejmij 13 - 6, więc wynik to 7. Nie możesz zmienić mianownika ułamka.
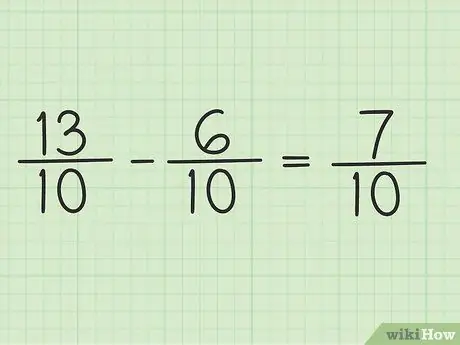
Krok 5. Napisz nowy licznik nad tym samym mianownikiem, aby uzyskać wynik końcowy
Nowy licznik to 7. Oba ułamki mają mianownik 10. Twój wynik końcowy to 7/10.
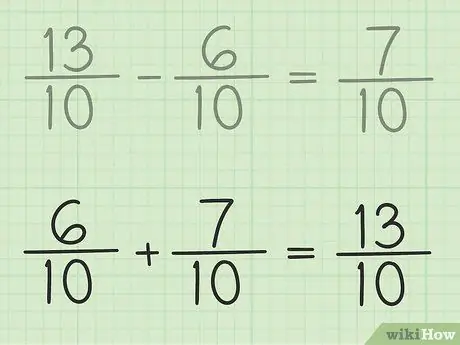
Krok 6. Sprawdź swoją pracę
Jeśli chcesz się upewnić, że poprawnie odejmujesz ułamek, po prostu zsumuj swoją odpowiedź i mniejszy ułamek, aby wynik był ułamkiem większym. 7/10 + 6/10 = 13/10. Jest skonczone.
Metoda 5 z 6: Odejmowanie ułamków od liczb całkowitych

Krok 1. Zapisz problem
Załóżmy na przykład, że chcesz rozwiązać następujący problem: 5 -. Zapisz to.
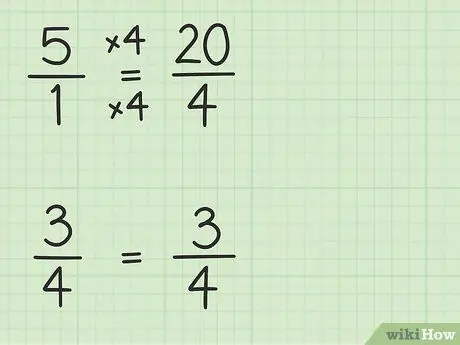
Krok 2. Konwertuj liczby całkowite na ułamki, które mają taki sam mianownik jak inne ułamki
Będziesz konwertować 5 na ułamek z mianownikiem 4, aby móc odjąć dwie liczby. Musisz więc myśleć o 5 jako ułamku 5/1. Następnie możesz pomnożyć licznik i mianownik nowego ułamka przez 4, aby mianowniki tych dwóch liczb były takie same. Więc 5/1 x 4/4 = 20/4. Ten ułamek jest równy 5, ale pozwala odjąć dwie liczby.
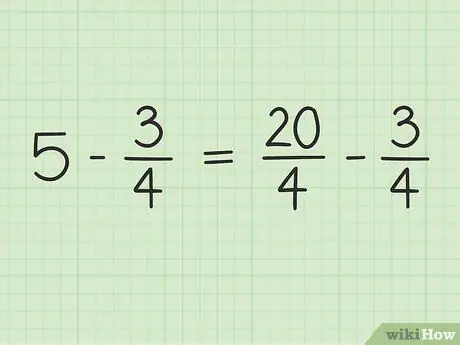
Krok 3. Przepisz problem
Nowy problem można zapisać tak: 20/4 - 3/4.
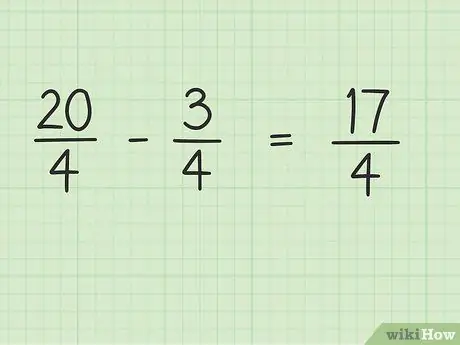
Krok 4. Odejmij licznik ułamka, podczas gdy mianownik pozostaje taki sam
Teraz po prostu odejmij 20 przez 3, aby uzyskać ostateczny wynik. 20 - 3 = 17, więc 17 to nowy licznik. Możesz zostawić mianownik bez zmian.
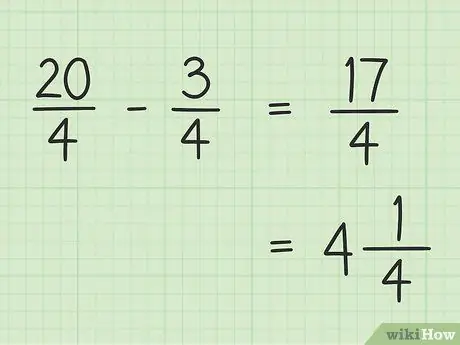
Krok 5. Zapisz swój wynik końcowy
Twój końcowy wynik to 17/4. Jeśli chcesz zapisać to jako liczbę mieszaną, podziel 17 przez 4 tak, aby wynik był 4, a reszta to 1, aby końcowa 17/4 równała się 4.
Metoda 6 z 6: Odejmowanie zmiennych
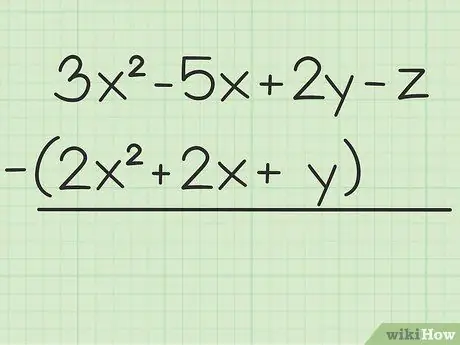
Krok 1. Zapisz problem, który chcesz rozwiązać
Na przykład następujące pytanie: 3x2 - 5x + 2 lata - z - (2x2 + 2x + y). Napisz pierwszy zestaw zmiennych na drugim.
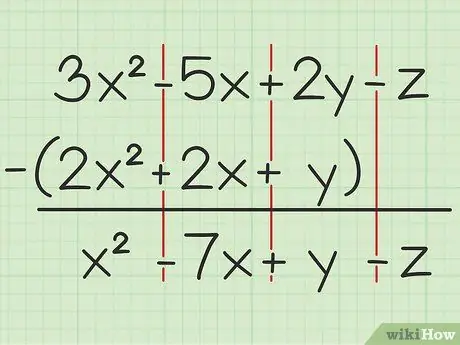
Krok 2. Odejmij te same zmienne
Jeśli napotkasz zmienną, możesz tylko dodać lub odjąć tę samą zmienną, która jest zapisana z tym samym stopniem kwadratu. Oznacza to, że możesz odjąć 4x2 od 7x2, ale nie może odjąć 4x od 4 lat. Możesz więc rozwiązać problem w ten sposób:
- 3x2 - 2x2 = x2
- -5x - 2x = -7x
- 2y - y = y
- -z - 0 = -z
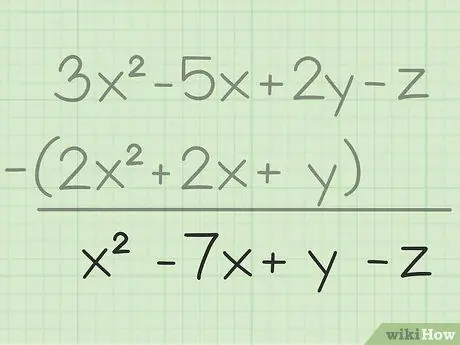
Krok 3. Zapisz swój wynik końcowy
Odjąłeś wszystkie te same zmienne, wszystko, co musisz zrobić, to napisać wynik końcowy, który będzie zawierał wszystkie odjęte przez Ciebie zmienne. Oto efekt końcowy:






