Dla większości ludzi ułamki są pierwszymi skomplikowanymi obliczeniami, na jakie można się natknąć. Koncepcja ułamków jest dość trudna i wymaga nauczenia się specjalnych warunków, aby to zrobić. Ponieważ ułamki mają specjalne zasady dodawania, odejmowania, mnożenia i dzielenia, wiele osób jest z tym zdezorientowanych. Jednak przy dużej praktyce każdy może nauczyć się i wykonywać obliczenia związane z ułamkami.
Krok
Metoda 1 z 5: Zrozumienie ułamków
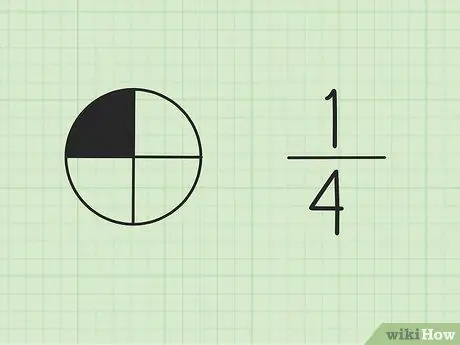
Krok 1. Zrozum, że ułamki są częścią całości
Liczba u góry nazywana jest licznikiem i reprezentuje liczbę części sumy. Liczba na dole nazywana jest mianownikiem, który reprezentuje całkowitą liczbę części.
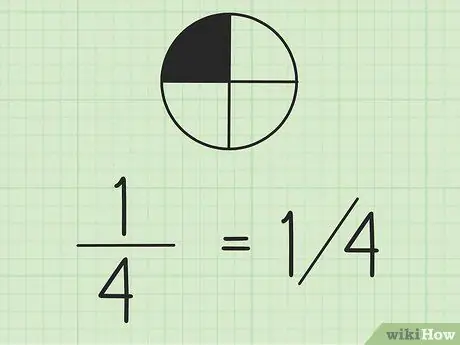
Krok 2. Pamiętaj, że możesz pisać ułamki za pomocą ukośników
Liczba po lewej stronie to licznik, a liczba po prawej to mianownik. Jeśli pracujesz z ułamkami w tym samym wierszu, dobrym pomysłem jest napisanie licznika nad mianownikiem.
Na przykład, jeśli weźmiesz jeden z czterech kawałków pizzy, masz pizzę. Jeśli masz 7/3 pizzy, oznacza to, że masz dwie całe pizze plus 1 z 3 kawałków pizzy
Metoda 2 z 5: Różnica między ułamkami mieszanymi i prostymi
Krok 1. Zrozum, że liczby mieszane składają się z liczb całkowitych i ułamków, na przykład 2 1/3 lub 45 1/2
Zwykle musisz przekonwertować liczby mieszane na prostszą formę, aby dodać, odjąć, mnożyć lub dzielić.
Krok 2. Zmień liczbę mieszaną, mnożąc liczbę całkowitą przez mianownik w ułamku, a następnie dodając ją przez licznik
Zapisz wynik jako licznik, a mianownik się nie zmienia.
Na przykład, aby przekonwertować 2 1/3 na ułamek prosty, pomnóż 2 przez 3, a następnie dodaj 1 i uzyskaj 7/3
Krok 3. Konwertuj proste ułamki na liczby mieszane, dzieląc licznik przez mianownik
Cały wynik dzielenia jest zapisywany jako liczba całkowita, a pozostała część dzielenia jest zapisywana jako licznik ułamka. Mianownik się nie zmienia.
Na przykład, aby przekonwertować 7/3 na liczbę mieszaną, podziel 7 przez 3, aby otrzymać 2 z resztą 1. Zatem liczba mieszana to 2 1/3. Ułamki proste można przekonwertować na liczby mieszane tylko wtedy, gdy licznik jest większy niż mianownik
Metoda 3 z 5: Dodawanie i odejmowanie ułamków
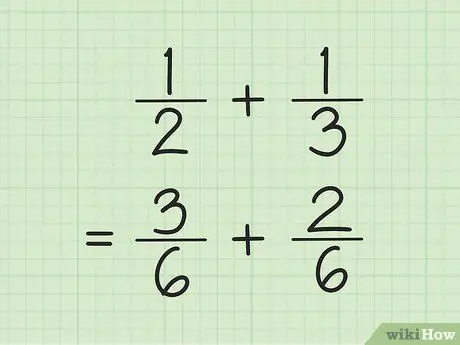
Krok 1. Znajdź wspólny mianownik do dodawania i odejmowania ułamków
Sztuczka, pomnóż liczby w mianowniku, a następnie pomnóż każdy licznik przez liczbę użytą do znalezienia mianownika. Czasami można znaleźć LCM (najmniejszą wspólną wielokrotność) dla mianownika, mnożąc mianowniki przez siebie.
Na przykład, aby dodać i 1/3, najpierw znajdź LCM (najmniejszą wspólną wielokrotność) dwóch mianowników, mnożąc się nawzajem. Zatem mnożysz 2 i 3, aby uzyskać LCM 6. Pomnóż 1 przez 3, aby uzyskać 3 jako nowy licznik pierwszego ułamka. Pomnóż 1 przez 2, aby otrzymać 2 jako nowy licznik drugiego ułamka. Twoje nowe frakcje to 3/6 i 2/6
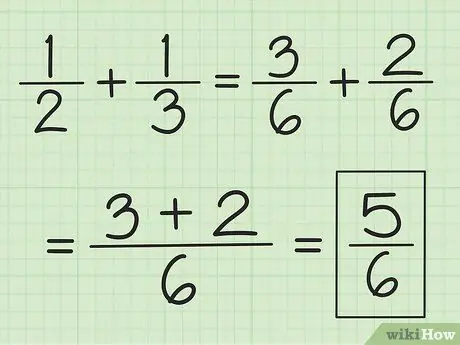
Krok 2. Dodaj dwa liczniki razem i nie zmieniaj mianownika
Na przykład 3/6 plus 2/6 to 5/6, a 2/6 plus 1/6 to 3/6
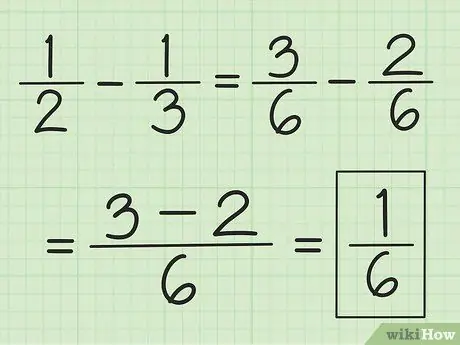
Krok 3. Użyj podobnej techniki do odejmowania
Najpierw znajdź LCM mianowników, ale zamiast je sumować, odejmij liczbę pierwszego licznika od liczby drugiego.
Na przykład, aby odjąć 1/3 od 1/2, najpierw zmień ułamki na 3/6 i 2/6, a następnie odejmij 3 przez 2, aby uzyskać 1. Daje to 1/6
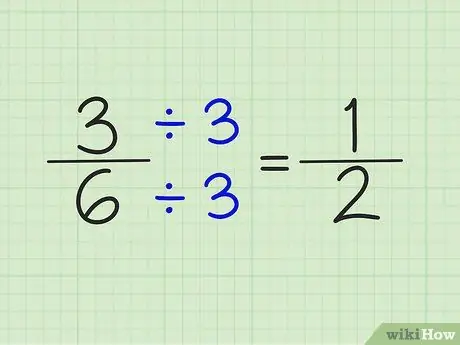
Krok 4. Uprość ułamki, dzieląc licznik i mianownik przez tę samą liczbę
Na przykład liczby 5/6 nie można uprościć. Jednak 3/6 można uprościć, dzieląc licznik i mianownik przez liczbę 3. Wynik jest ułamkiem 1/2
Krok 5. Przekształć ułamek na liczbę mieszaną, jeśli licznik jest większy niż mianownik
Metoda 4 z 5: Mnożenie i dzielenie ułamków
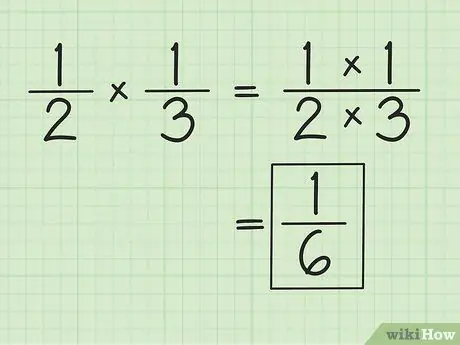
Krok 1. Pomnóż oddzielnie licznik i mianownik, aby pomnożyć ułamki
Na przykład po mnożeniu i 1/3 wynik to 1/6 (1 razy 1 i 2 razy 3). Nie musisz dopasowywać mianowników podczas mnożenia ułamków. W razie potrzeby uprość lub zmodyfikuj uzyskane wyniki
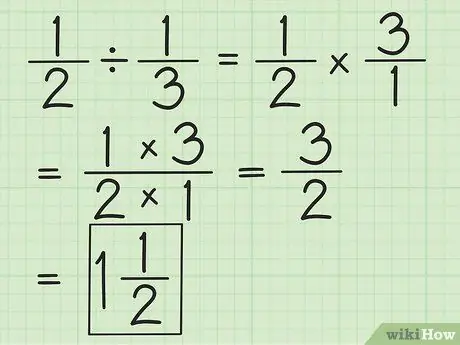
Krok 2. Podziel dwie frakcje, odwracając drugą frakcję, a następnie mnożąc obie
Na przykład, jeśli chcesz podzielić 1/2 przez 1/3, najpierw odwróć drugą część na 3/1. Pomnóż przez 3/1 i uzyskaj 3/2. Uprość ułamki lub przekonwertuj na liczby mieszane, jeśli to możliwe
Metoda 5 z 5: Praca z ułamkami złożonymi
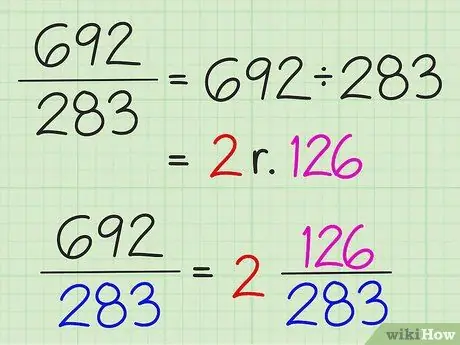
Krok 1. Przepracuj wszystkie ułamki w ten sam sposób, nawet jeśli problem wydaje się bardzo skomplikowany
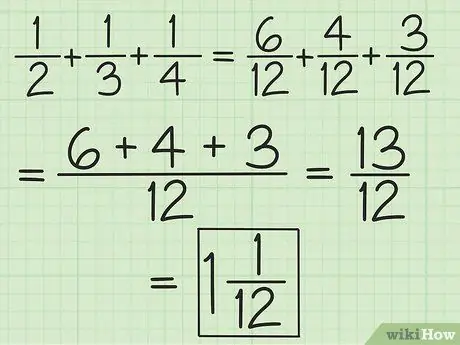
Krok 2. Dopasuj mianowniki dla wszystkich ułamków lub pracuj w parach, zaczynając od lewej do prawej, aby dodać i odjąć więcej niż dwa ułamki
Na przykład, aby dodać 1/2, 1/3 i 1/4, możesz zmienić je na 6/12, 4/12 i 3/12, aby uzyskać 13/12, lub możesz dodać 3/6 i 2 /6, więc otrzymasz 5/6, a następnie dodaj 5/6 i 1/4 (wyrównaj mianowniki tak, aby druga część stała się 3/12), aby uzyskać 13/12 (10/12 plus 3/12). Przekształć go w liczbę mieszaną, czyli 1 1/12
Porady
- Pamiętaj, że nauczyłeś się całkiem sporo matematyki. Matematyka jest jak język, który możesz płynnie wymawiać, a teraz próbujesz nauczyć się go czytać i pisać.
- Pamiętaj, aby zawsze uprościć końcowy wynik obliczeń, niezależnie od tego, czy problem ma postać ułamka zwykłego, liczby mieszanej czy ułamka złożonego.
