Liczenie ułamków to jedna z najbardziej przydatnych umiejętności matematycznych do rozwijania. Przed wykonaniem obliczeń ułamkowych naucz się identyfikować części i typy ułamków. Następnie możesz je dodawać lub odejmować. Aby uzyskać bardziej złożone obliczenia, dowiedz się, jak mnożyć i dzielić ułamki. Zwykle będziesz także musiał uprościć lub zmniejszyć ułamki.
Krok
Metoda 1 z 4: Rozpoznawanie ułamków
Krok 1. Znajdź ułamek
Ułamki są zapisywane jako jedna liczba powyżej linii podziału, a druga liczba poniżej linii.
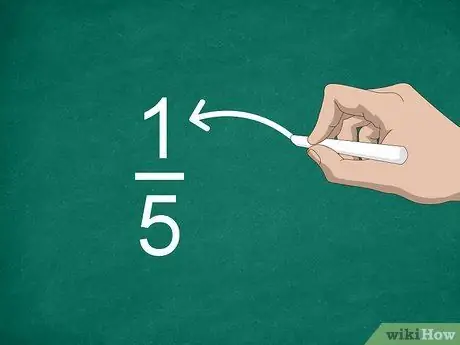
Krok 2. Zidentyfikuj licznik
Liczba nad linią nazywana jest licznikiem i pokazuje, ile części znajduje się w ułamku.
Na przykład w ułamku 1/5 „1” jest licznikiem
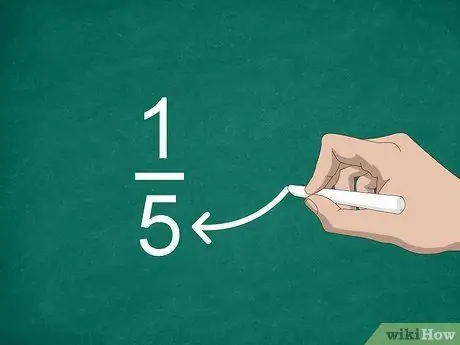
Krok 3. Znajdź mianownik
Liczba umieszczona poniżej linii nazywana jest mianownikiem. Ta wartość wskazuje liczbę części, które „konstruują” liczbę całkowitą.
Na przykład w ułamku 1/5 „5” jest mianownikiem, więc ułamek składa się z pięciu części
Krok 4. Określ, czy ułamki są ułamkami rozsądnymi czy ułamkami niewłaściwymi
Jeśli licznik jest mniejszy niż mianownik, ułamek jest ułamkiem naturalnym. W ułamkach niewłaściwych licznik jest większy niż mianownik.
- Na przykład 3/4 to rozsądny ułamek, a 5/3 to ułamek niewłaściwy.
- Jeśli masz liczbę całkowitą, która zawiera ułamek, liczba ta jest nazywana liczbą mieszaną. Na przykład 1 1/2 to liczba mieszana.
Metoda 2 z 4: Dodaj lub odejmij ułamki
Krok 1. Zidentyfikuj ułamki o tym samym mianowniku
Jeśli musisz dodać lub odjąć ułamki, każdy ułamek musi mieć ten sam mianownik przed wykonaniem obliczeń. Obserwuj mianownik każdego ułamka, aby upewnić się, że wszystkie są równe (podobne).
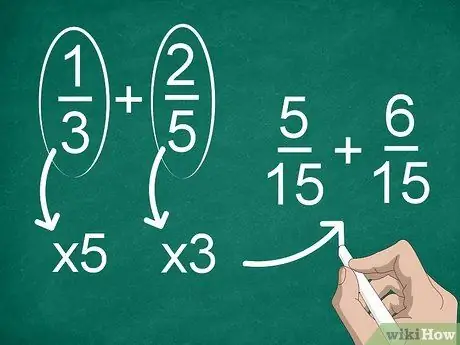
Krok 2. Znajdź wspólny mianownik, jeśli każda frakcja ma inny mianownik
Jeśli mianowniki nie są takie same, musisz zmienić ułamki, aby miały ten sam mianownik. Aby znaleźć wspólny mianownik, pomnóż każdy ułamek przez mianownik drugiego.
Na przykład, aby znaleźć wspólny mianownik w 1/3 + 2/5, pomnóż „1” i „3” przez „5”, a następnie pomnóż „2” i „5” przez „3”. Teraz masz dodanie 5/15 + 6/15. Następnie możesz obliczyć ułamki
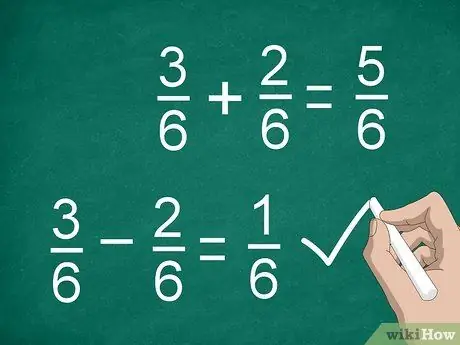
Krok 3. Dodaj lub odejmij liczniki, aby obliczyć ułamki
Po znalezieniu wspólnego mianownika i pomnożeniu liczników (jeśli to konieczne) możesz dodawać lub odejmować. Dodaj lub odejmij liczniki i umieść wynik nad linią podziału. Wpisz wspólny mianownik poniżej linii.
- Na przykład 3/6 - 2/6 = 1/6.
- Nie dodawaj ani nie odejmuj mianowników.
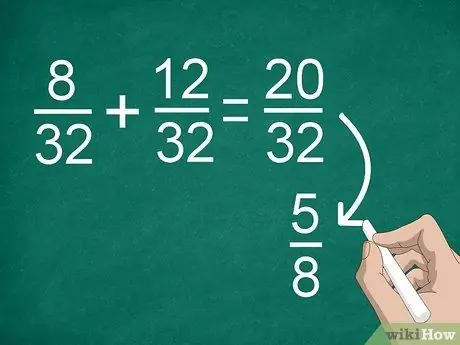
Krok 4. W razie potrzeby uprość wyniki
Jeśli wcześniej musiałeś znaleźć wspólny mianownik, możesz otrzymać duży ułamek, który możesz uprościć. Na przykład, jeśli dodasz 8/32 +12/32, otrzymasz jako wynik „20/32”. Ten ułamek można uprościć do „5/8”.
Metoda 3 z 4: Mnożenie i upraszczanie ułamków
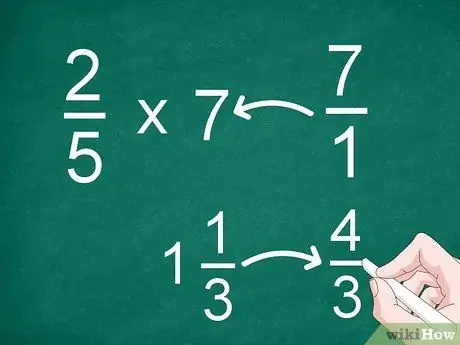
Krok 1. Przekształć ułamki mieszane lub liczby całkowite na ułamki niewłaściwe
Aby ułatwić mnożenie, musisz przekonwertować każdą liczbę na rozsądny lub niewłaściwy ułamek. Jeśli masz liczby całkowite lub mieszane, które musisz pomnożyć, najpierw zamień je na ułamek zwykły (naturalny lub niewłaściwy).
- Na przykład, aby pomnożyć 2/5 przez 7, zamień „7” na ułamek. Następnie możesz pomnożyć 2/5 przez 7/1.
- Jeśli masz liczbę mieszaną, taką jak 1 1/3, zamień ją na ułamek niewłaściwy („4/3”) przed pomnożeniem.
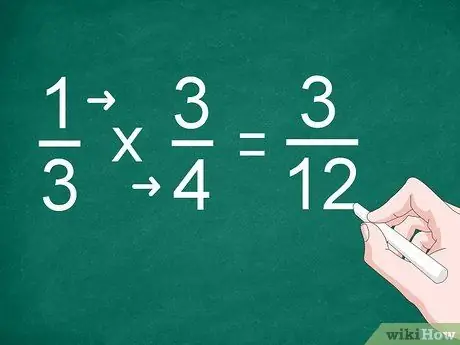
Krok 2. Pomnóż każdy licznik i mianownik
Zamiast dodawać, pomnóż licznik i wpisz wynik powyżej linii podziału. Musisz również pomnożyć mianowniki i napisać wynik poniżej linii.
Na przykład, aby pomnożyć 1/3 przez 3/4, pomnóż „1” przez „3”, aby uzyskać licznik. Pomnóż „3” przez „4”, aby otrzymać mianownik. Odpowiedź na mnożenie to „3/12”
Krok 3. Uprość wyniki
Zwykle będziesz musiał zredukować wynik do prostszej formy, zwłaszcza jeśli początkowo masz nienaturalne ułamki. Znajdź największy wspólny dzielnik i użyj tego współczynnika, aby uprościć licznik i mianownik.
Na przykład dla ułamka 3/12 największym wspólnym dzielnikiem między „3” i „12” jest „3”. Podziel każdy element ułamka przez „3”, aż uzyskasz ułamek „1/4”
Metoda 4 z 4: Podziel ułamki
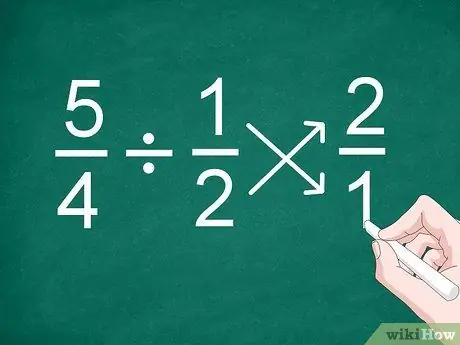
Krok 1. Odwróć pozycję drugiej frakcji
Najłatwiejszym sposobem dzielenia ułamków, nawet ułamków o różnych mianownikach, jest odwrócenie pozycji drugiego ułamka przed obliczeniem wyniku.
Na przykład w przypadku problemu 5/4 1/2 odwróć pozycję ułamka „1/2” na „2/1”
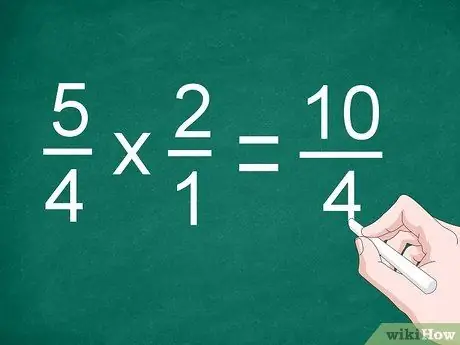
Krok 2. Pomnóż licznik i mianownik
Pomnóż ułamki bezpośrednio, aby pomnożyć liczniki. Zapisz wynik nad linią podziału, a następnie pomnóż mianownik. Zapisz iloczyn mianowników poniżej linii.
W poprzednim przykładzie pomnóż 5/4 przez 2/1, aby otrzymać „10/4”
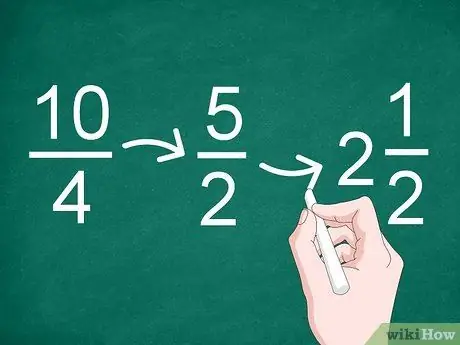
Krok 3. W razie potrzeby uprość wyniki
Jeśli wynik dzielenia jest ułamkiem niewłaściwym lub można go zmniejszyć, uprość ułamek. Użyj największego wspólnego współczynnika, aby zmniejszyć ułamek.
- Na przykład największym wspólnym dzielnikiem ułamka 10/4 jest „2”, więc wynik uproszczenia to „5/2” (10 podzielone przez 2 i 4 podzielone przez 2).
- Ponieważ wynikiem uproszczenia jest ułamek niewłaściwy, można go przekonwertować na liczbę całkowitą i ułamek (liczba mieszana). Dlatego 5/2 można zmienić na „2”.
Porady
- Jeśli pracujesz z ułamkami złożonymi, musisz wykonać kilka dodatkowych kroków, aby uprościć ułamek. Jednak samo to uproszczenie jest obowiązkową częścią procesu obliczeniowego.
- Zawsze pisz starannie ułamki, aby zmniejszyć ryzyko błędnych obliczeń.
