- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:32.
- Ostatnio zmodyfikowany 2025-01-23 12:43.
Jeśli już rozumiesz, konwersja zwykłych ułamków zwykłych na ułamki dziesiętne nie jest trudna. Aby przekonwertować zwykłe ułamki zwykłe na ułamki dziesiętne, możesz użyć długiego dzielenia, mnożenia, a nawet kalkulatora, jeśli nie chcesz wykonywać obliczeń ręcznie. Po opanowaniu metody będziesz mógł łatwo konwertować ułamki zwykłe na ułamki dziesiętne.
Krok
Metoda 1 z 4: Z dzieleniem długim
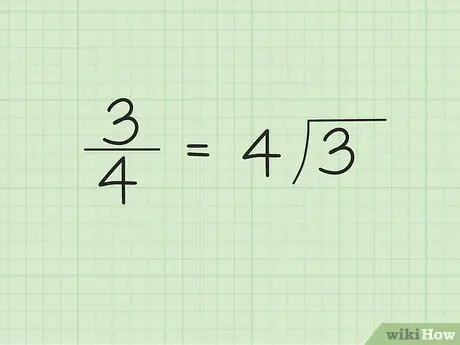
Krok 1. Wpisz mianownik na zewnątrz/lewa strona symbolu dzielnika i licznik wewnątrz/prawa strona symbolu dzielnika
Załóżmy na przykład, że chcemy przekonwertować 3/4 na ułamek dziesiętny. Wpisz „4” na zewnątrz/lewa strona symbolu dzielnika i „3” wewnątrz/prawa strona symbolu dzielnika. „4” to liczba, która się dzieli, a „3” to liczba, która jest dzielona.

Krok 2. Napisz „0”, a następnie kropkę dziesiętną (przecinek), nad symbolem dzielnika
Ponieważ liczy się ułamek, wynik musi być mniejszy niż jeden, więc ten krok jest bardzo ważny. Następnie wpisz znak dziesiętny, a następnie „0”, po cyfrze „3” po prawej stronie symbolu dzielnika. Mimo że „3” równa się „3, 0”, zero pozwala na podzielenie „3, 0” przez „4”.

Krok 3. Oblicz odpowiedź używając długiego dzielenia
Przy długim dzieleniu na razie znak dziesiętny można zignorować, więc wystarczy obliczyć 30 podzielone przez 4. Oto jak:
- Najpierw podziel 3, 0, co daje 30, przez 4. Najbliższe 4 do 30 to 4 x 7 = 28, pozostawiając 2. Więc napisz „7” po „0” nad dzielnikiem i „28” pod „ 3, 0” w/prawa strona symbolu dzielnika. Poniżej 28 lat napisz „2”, reszta 30 minus 28.
- Następnie wpisz „0” po „3, 0”, tak aby stało się „3, 00”, co można uznać za „300”, po wewnętrznej/prawej stronie symbolu dzielnika. W ten sposób 0 można obniżyć na prawo od „2”, aby „20” było podzielne przez „4”.
- „20” podzielone przez „4” równa się „5”. Tak więc wpisz „5” po „0.7” nad symbolem dzielnika, tak aby stało się „0.75”.

Krok 4. Napisz ostateczną odpowiedź
Tak więc „3” podzielone przez „4” równa się „0,75”. Zapisz odpowiedź. Skończone.
Metoda 2 z 4: Ułamki generujące powtarzające się ułamki dziesiętne
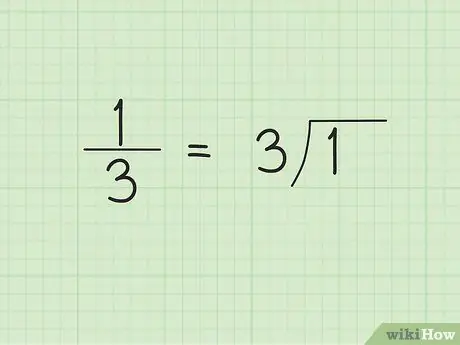
Krok 1. Dokonaj dzielenia przez długi czas
Rozpoczynając dzielenie długich cyfr, możesz nie być w stanie przewidzieć, że wynik będzie powtarzalną liczbą dziesiętną. Załóżmy na przykład, że chcemy przekonwertować ułamek zwykły 1/3 na postać dziesiętną. Napisz 3 lub mianownik po zewnętrznej/lewej stronie symbolu dzielnika i 1 wewnątrz/po prawej stronie symbolu dzielnika.

Krok 2. Napisz 0, a następnie znak dziesiętny nad symbolem dzielnika
Ponieważ wynik musi być mniejszy niż 1, ten krok przygotowuje odpowiedź do zapisania w postaci dziesiętnej. Znak dziesiętny należy również wpisać po prawej stronie liczby „1”, która znajduje się po prawej stronie symbolu dzielnika.
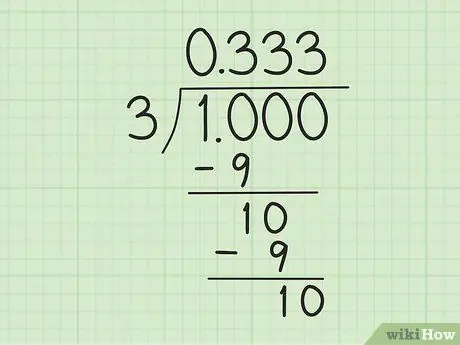
Krok 3. Zacznij obliczać dzielenie przez długie dzielenie
Zacznij od przekształcenia „1” w „1, 0”, które liczy się jako „10”, tak aby była podzielna przez „3”. Następnie wykonaj następujące czynności:
- Podziel 10 przez 3. Użyj 3 x 3 = 9, aby otrzymać resztę 1. Napisz więc 3 na prawo od „0” nad symbolem dzielnika i odejmij 10 przez 9, aby otrzymać resztę z 1.
- Wpisz „0” po prawej stronie liczby „1” (pozostała część 10 minus 9 w poprzednim kroku), aby uzyskać kolejne „10”. Przy ponownym dzieleniu „10” przez „3” powtarza się ten sam proces: wpisz „3” po prawej stronie pierwszej „3” nad symbolem dzielnika i odejmij nową „10” od „9”.
- Kontynuuj, aż utworzy się wzór. Wiesz, że coś jest dziwnego? Ten podział może trwać wiecznie. 10 jest zawsze podzielne przez 3: zawsze będzie „1” na dole i nowa „3” po przecinku nad symbolem dzielnika.
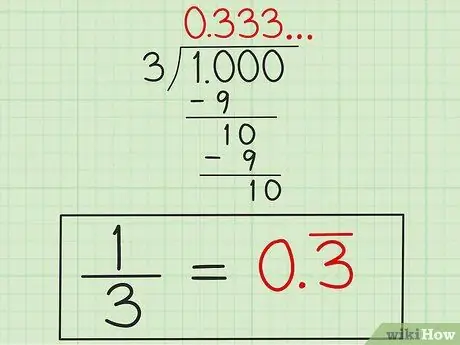
Krok 4. Napisz odpowiedź
Wiedząc, że „3” się powtórzy, wpisz odpowiedź „0, 3” z linią nad cyfrą „3” (lub „0, 33” z linią nad obiema cyframi „3”) jako wskazanie, że numer „3” powtarza się. Ta odpowiedź jest w postaci dziesiętnej 1/3, ponieważ 1 podzielone przez 3 nie zakończy się samo.
Istnieje wiele ułamków, które dają powtarzające się ułamki dziesiętne, takie jak 2/9 („0, 2” z powtarzaniem „2”), 5/6 („0, 83” z powtarzaniem „3”) lub 7/9 („0, 7” z „7” ciągle się powtarza). Ten wzorzec występuje zawsze, gdy mianownik jest wielokrotnością 3, a licznik nie może być podzielny przez mianownik
Metoda 3 z 4: przez mnożenie

Krok 1. Znajdź liczbę, którą można pomnożyć przez mianownik ułamka, aby otrzymać 10, 100, 1000 lub dowolną liczbę o podstawie 10
Może to być łatwy sposób na konwersję ułamków zwykłych na ułamki dziesiętne bez używania długiego dzielenia lub kalkulatora. Najpierw znajdź liczbę, którą można pomnożyć przez mianownik ułamka, aby otrzymać 10, 100, 1000 i tak dalej. Aby to zrobić, najpierw podziel 10, potem 100, potem 1000 i tak dalej przez mianownik, aż otrzymasz liczbę całkowitą. Przykład:
- 3/5. 10/5 = 2,2 to liczba całkowita. 2 można pomnożyć przez 5, aby uzyskać 10. Czyli 2 można użyć.
- 3/4. 10/4 = 2, 5. 2, 5 nie jest liczbą całkowitą. 100/4 = 25. 25 jest liczbą całkowitą. 25 można pomnożyć przez 4, aby uzyskać 100. Zatem 25 można użyć.
- 5/16. 10/16 = 0,625, 100/16 = 6, 25, 1000/16 = 62, 5, 10 000/16 = 625. 625 jest pierwszą otrzymaną liczbą całkowitą. 625 można pomnożyć przez 16, aby otrzymać 10 000. Można więc użyć 625.
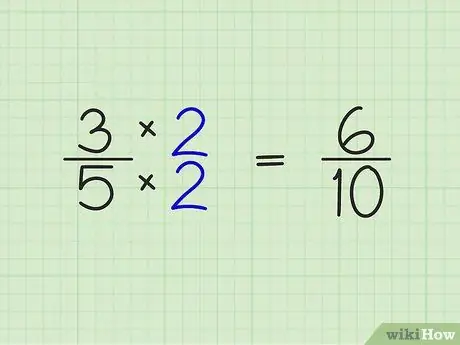
Krok 2. Pomnóż licznik i mianownik ułamka przez liczbę całkowitą uzyskaną w poprzednim kroku
Ten krok jest dość łatwy. Po prostu pomnóż liczby powyżej i poniżej ułamka przez liczbę całkowitą uzyskaną w poprzednim kroku. Przykład:
- 3/5 x 2/2 = 6/10
- 3/4 x 25/25 = 75/100
- 5/16 x 625/625 = 3,125/10000

Krok 3. Napisz ostateczną odpowiedź
Odpowiedź jest taka, że licznik jest oznaczony ułamkiem dziesiętnym zgodnie z liczbą zer w mianowniku. Po prostu policz, ile zer znajduje się w mianowniku. Jeśli w mianowniku jest tylko 10, przesuń kropkę dziesiętną w lewo o 1 cyfrę i tak dalej. Przykład:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
Metoda 4 z 4: Z kalkulatorem

Krok 1. Podziel licznik przez mianownik
Ta metoda jest bardzo prosta. Po prostu użyj kalkulatora, aby podzielić licznik, liczbę na górze ułamka, przez mianownik, liczbę na dole ułamka. Załóżmy na przykład, że chcesz przekonwertować 3/4 na ułamek dziesiętny. Wystarczy nacisnąć „3”, następnie symbol dzielenia („÷”), następnie „4”, a na końcu symbol równości („= ).

Krok 2. Zapisz otrzymane odpowiedzi
Odpowiedź to 0,75, więc forma dziesiętna wspólnego ułamka 3/4 to 0,75.
Porady
- Aby sprawdzić, czy Twoja odpowiedź jest poprawna, pomnóż odpowiedź przez mianownik ułamka. Jeśli Twoja odpowiedź jest poprawna, iloczyn mnożenia jest licznikiem ułamka.
- Niektóre ułamki można przekonwertować na ułamki dziesiętne, tworząc porównywalne ułamki, których mianowniki mają podstawę 10 (10, 100, 1000 itd.). Następnie użyj wartości miejsc, aby zapisać poprawną formę dziesiętną.






