- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:21.
- Ostatnio zmodyfikowany 2025-01-23 12:43.
Dzielenie ułamka przez ułamek może początkowo wydawać się mylące, ale w rzeczywistości jest bardzo łatwe. Wystarczy odwrócić, pomnożyć i uprościć! Ten artykuł przeprowadzi Cię przez proces i pokaże, jak łatwo jest podzielić ułamek przez ułamek.
Krok
Część 1 z 2: Zrozumienie, jak dzielić ułamki przez ułamki
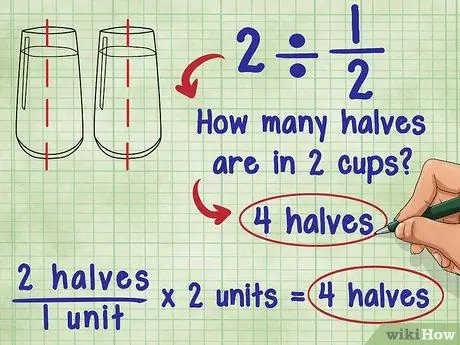
Krok 1. Zastanów się, co oznacza dzielenie przez ułamek
O 2 ÷ 1/2 zapytała Ada: "Ile połówek jest w 2?" Odpowiedź to 4, ponieważ każda jednostka (1) składa się z dwóch „połówek”, a są 2 jednostki: 2 „połowa”/1 jednostka * 2 jednostki = 4 „połowa”.
- Spróbuj wyobrazić sobie to samo równanie, używając szklanki wody: Ile i pół szklanki wody znajduje się w 2 szklankach wody? Do każdej szklanki wody można wlać 2 i pół szklanki wody. Oznacza to, że w zasadzie dodajesz „połowę” wody i masz dwie szklanki: 2 „połowa”/1 filiżanka * 2 filiżanki = 4 „połowa”.
- Oznacza to, że jeśli ułamek, który dzielisz, wynosi od 0 do 1, odpowiedź jest zawsze większa niż oryginalna liczba! Dzieje się tak, gdy dzielisz liczbę całkowitą lub ułamek przez ułamek.

Krok 2. Zrozum, że dzielenie jest przeciwieństwem mnożenia
Zatem dzielenie przez ułamek można rozwiązać, mnożąc przez odwrotność ułamka. Odwrotność ułamka (nazywana również „odwrotnością mnożenia”) to ułamek, który jest odwrócony, tak że licznik i mianownik zamieniają się miejscami. Za chwilę będziemy dzielić ułamki przez ułamki, znajdując odwrotność drugiego ułamka i mnożąc oba ułamki. Spójrzmy jednak najpierw na niektóre przeciwieństwa:
- Odwrotność 3/4 to 4/3.
- Przeciwieństwem 7/5 jest 5/7.
- Odwrotność 1/2 to 2/1 lub 2.
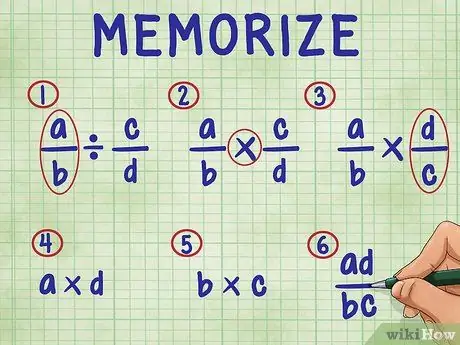
Krok 3. Zapamiętaj następujące kroki, aby podzielić ułamek przez ułamek
W kolejności kroki obejmują:
- Po prostu zostaw pierwszy ułamek w równaniu.
- Zmień znak dzielenia na znak mnożenia.
- Odwróć drugą część (znajdź jej odwrotność).
- Pomnóż licznik (górną liczbę) obu ułamków. Wynik mnożenia to licznik (na górze) Twojej odpowiedzi.
- Pomnóż mianownik (dolna liczba) obu ułamków. Iloczyn produktu jest mianownikiem Twojej odpowiedzi.
- Uprość swoje ułamki, upraszczając je do najprostszych terminów.
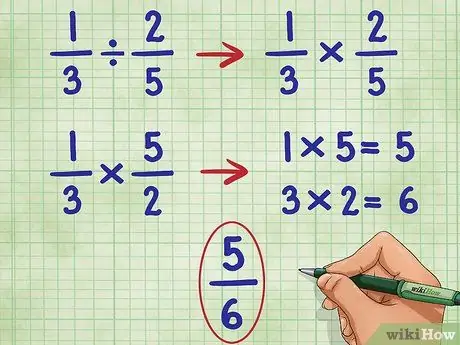
Krok 4. Wykonaj te kroki dla przykładu 1/3 2/5
Zaczniemy od pominięcia pierwszego ułamka i zamiany znaku dzielenia na znak mnożenia:
- 1/3 ÷ 2/5 = Staje się:
- 1/3 * _ =
- Teraz odwracamy drugi ułamek (2/5), aby znaleźć jego odwrotność, czyli 5/2:
- 1/3 * 5/2 =
- Teraz pomnóż licznik (górną liczbę) obu ułamków, 1*5 = 5.
- 1/3 * 5/2 = 5/
- Teraz pomnóż mianownik (dolna liczba) obu ułamków, 3*2 = 6.
- Teraz mamy: 1/3 * 5/2 = 5/6
- Tego ułamka nie da się dalej uprościć, więc mamy odpowiedź.

Krok 5. Spróbuj zapamiętać następujące rymy, które pomogą Ci zapamiętać:
„Dzielenie ułamków jest łatwe, odwróć drugi ułamek, a następnie pomnóż. Nie zapomnij uprościć, zanim nadejdzie czas na jedzenie”.
Kolejna pomocna pomoc przypomnienia informuje, co zrobić z każdą częścią równania: „Pozwól mi (pierwszy ułamek), Zmień mnie (znak podziału), Odwróć mnie (drugi ułamek).”
Część 2 z 2: Dzielenie ułamków przez ułamki w problemach
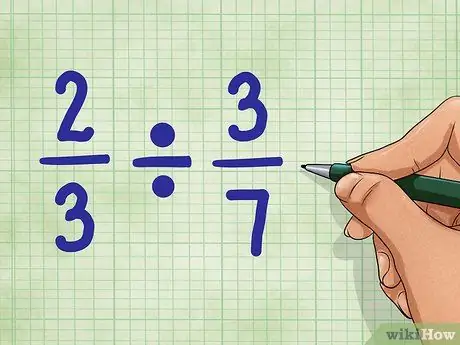
Krok 1. Zacznij od przykładowych pytań
Użyjmy 2/3 ÷ 3/7. To pytanie dotyczy liczby części równej 3/7, którą można znaleźć w wartości 2/3. Nie martw się. To nie jest takie trudne, jak się wydaje!
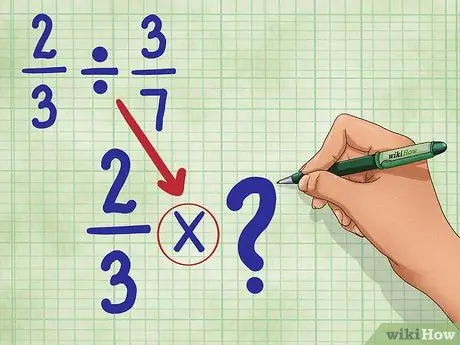
Krok 2. Zamień znak dzielenia na znak mnożenia
Twoje nowe równanie będzie: 2/3 * _ (Za chwilę wypełnimy to pole.)
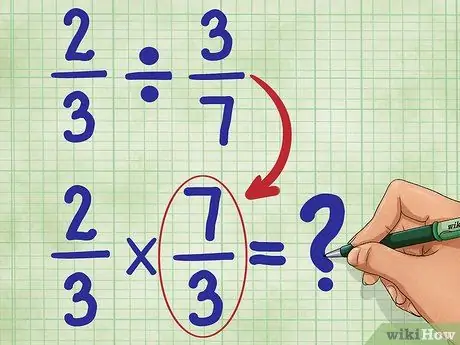
Krok 3. Teraz znajdź odwrotność drugiej frakcji
Oznacza to odwrócenie 3/7 tak, aby licznik (3) znajdował się teraz na dole, a mianownik (7) na górze. Odwrotność 3/7 to 7/3. Teraz napisz swoje nowe równanie:
2/3 * 7/3 = _

Krok 4. Pomnóż swoje ułamki
Najpierw pomnóż liczniki obu ułamków: 2 * 7 = 14. 14 to licznik (najwyższy numer) Twojej odpowiedzi. Następnie pomnóż mianowniki obu ułamków: 3 * 3 = 9. 9 to mianownik (dolna liczba) Twojej odpowiedzi. Teraz wiesz, że 2/3 * 7/3 = 14/9.
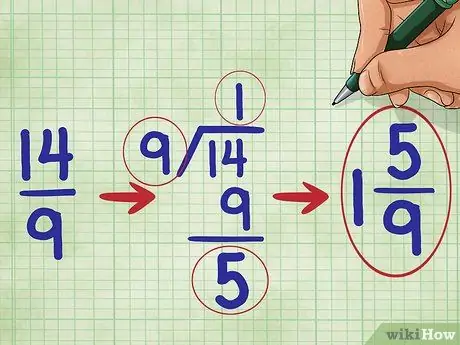
Krok 5. Uprość swoją frakcję
W tym problemie, ponieważ licznik ułamka jest większy niż mianownik, wiemy, że nasz ułamek jest większy niż 1. Musimy go przeliczyć na liczbę mieszaną. (Liczba mieszana to łączna liczba i ułamek, na przykład 1 2/3.))
-
Najpierw podziel licznik
Krok 14. z 9.
Liczba 14 podzielona przez 9 równa się jeden z resztą 5, więc powinieneś zapisać swój uproszczony ułamek jako: 1 5/9 („jeden pięć dziewiąty”).
- Przestań, znalazłeś odpowiedź! Możesz określić, że nie możesz już uprościć ułamka, ponieważ mianownik nie jest podzielny przez licznik (9 nie jest podzielne przez 5), a licznik jest liczbą pierwszą lub liczbą całkowitą, która jest podzielna tylko przez jeden i samą liczbę.
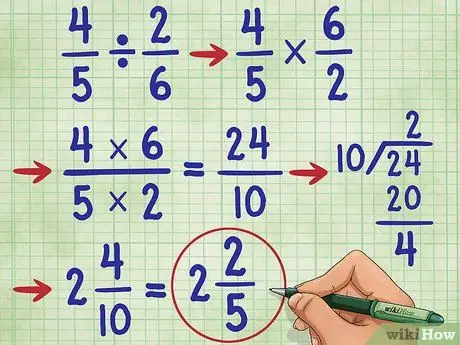
Krok 6. Wypróbuj inny przykład
Spróbujmy pytanie 4/5 ÷ 2/6 =. Najpierw zmień znak dzielenia na znak mnożenia (4/5 * _ =), a następnie znajdź odwrotność 2/6, czyli 6/2. Teraz masz równanie: 4/5 * 6/2 =_. Teraz pomnóż licznik, 4 * 6 = 24i mianownik 5* 2 = 10. Teraz masz 4/5 * 6/2 = 24/10.
Teraz uprość ułamek. Ponieważ licznik jest większy niż mianownik, musimy zamienić ten ułamek na liczbę mieszaną.
- Najpierw podziel licznik przez mianownik (24/10 = 2 pozostałe 4).
- Napisz odpowiedź jako 2 4/10. Możemy jeszcze raz uprościć ten ułamek!
- Zauważ, że 4 i 10 to liczby parzyste. Tak więc pierwszym krokiem do uproszczenia jest podzielenie każdej liczby przez 2. Otrzymujemy 2/5.
- Ponieważ mianownik (5) nie jest podzielny przez licznik (2), a 5 jest liczbą pierwszą, wiemy, że tego ułamka nie da się dalej uprościć. Tak więc nasza odpowiedź brzmi: 2 2/5.

Krok 7. Uzyskaj dodatkową pomoc w uproszczeniu ułamków
Prawdopodobnie spędziłeś dużo czasu na nauce uproszczenia ułamków, zanim spróbujesz je podzielić. Jeśli jednak potrzebujesz odświeżenia lub innej pomocy, istnieją świetne artykuły online, które mogą być dla Ciebie bardzo pomocne.
Powiązane artykuły wikiHow
- Zamiana wspólnych ułamków na ułamki dziesiętne
- Obliczanie powierzchni koła
- Dzielenie wielomianów za pomocą dzielenia syntetycznego
- Dzielenie frakcji mieszanych






