Dzielenie ułamków przez liczby całkowite nie jest tak trudne, jak się wydaje. Aby podzielić ułamek przez liczbę całkowitą, wystarczy przekonwertować liczbę całkowitą na ułamek, znaleźć odwrotność ułamka i pomnożyć wynik przez pierwszy ułamek. Jeśli chcesz wiedzieć, jak to zrobić, wykonaj następujące kroki:
Krok
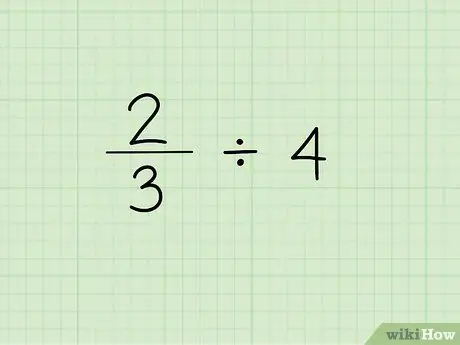
Krok 1. Zapisz problem
Pierwszym krokiem do podzielenia ułamka przez liczbę całkowitą jest napisanie ułamka, po którym następuje znak dzielenia i liczba całkowita potrzebna do podzielenia ułamka. Załóżmy, że pracujemy z następującym problemem: 2/3 4.
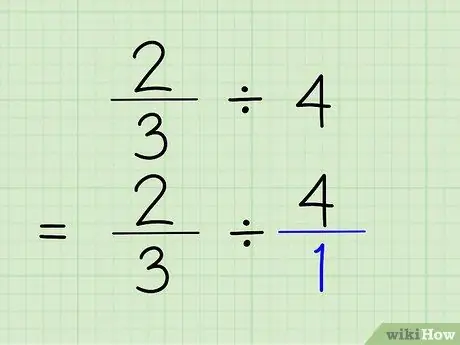
Krok 2. Konwersja liczb całkowitych na ułamki
Aby zamienić liczbę całkowitą na ułamek, wystarczy umieścić liczbę całkowitą nad liczbą 1. Liczba całkowita staje się licznikiem, a 1 staje się mianownikiem ułamka. Powiedzenie 4/1 to tak naprawdę to samo, co 4, ponieważ pokazujesz tylko, że liczba zawiera „1” 4 razy. Problemem będzie 2/3 4/1.
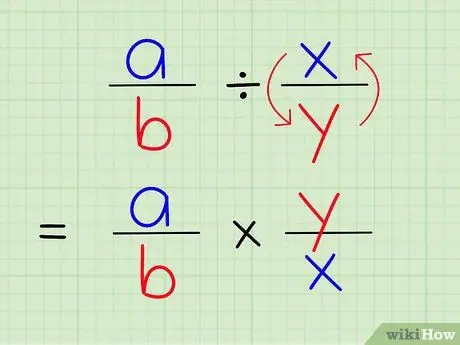
Krok 3. Dzielenie ułamka przez inny jest takie samo, jak pomnożenie tego ułamka przez odwrotność innego ułamka
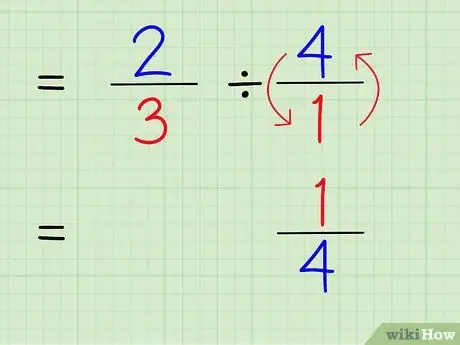
Krok 4. Napisz odwrotność liczby całkowitej
Aby znaleźć odwrotność liczby, zamień licznik i mianownik liczby. Dlatego, aby znaleźć odwrotność 4/1, po prostu zamień licznik i mianownik tak, aby liczba stała się 1/4.
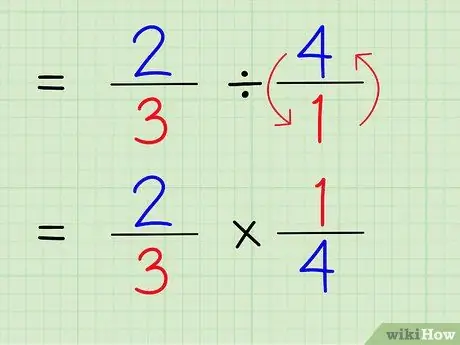
Krok 5. Zmień znak dzielenia na znak mnożenia
Problemem będzie 2/3 x 1/4.
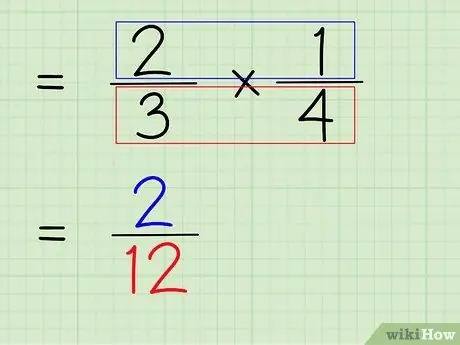
Krok 6. Pomnóż licznik i mianownik ułamka
Więc następnym krokiem jest pomnożenie licznika i mianownika ułamka, aby otrzymać nowy licznik i mianownik jako ostateczną odpowiedź.
- Aby pomnożyć liczniki, pomnóż 2 x 1, aby uzyskać 2.
- Aby pomnożyć mianowniki, wystarczy pomnożyć 3 x 4, aby otrzymać 12.
- 2/3 x 1/4 = 2/12
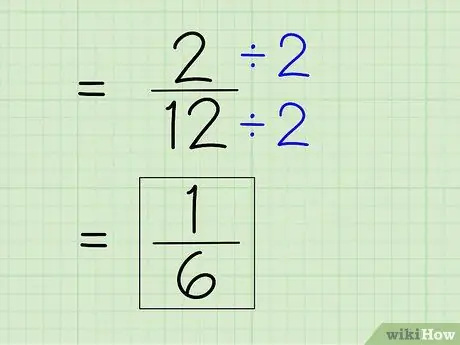
Krok 7. Uprość ułamek
Aby uprościć ułamek, musisz znaleźć najmniejszy mianownik, co oznacza, że musisz podzielić licznik i mianownik przez dowolną liczbę, która dzieli obie liczby. Ponieważ 2 jest licznikiem, musisz sprawdzić, czy 2 może całkowicie podzielić 12 -- może, ponieważ 12 jest liczbą parzystą. Następnie podziel licznik i mianownik przez 2, aby uzyskać nowy licznik i mianownik, aby uzyskać prostą odpowiedź.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- Ułamek 2/12 można uprościć do 1/6. To jest twoja ostateczna odpowiedź.
Porady
- Ma to wspomóc pamięć, łatwy sposób na zapamiętanie, jak wykonywać te wszystkie obliczenia. Pamiętaj o tym: „Łatwo jest dzielić ułamki, odwracać drugą liczbę i mnożyć!”
- Inną odmianą powyższej metody jest JGB/JBG. Nie zmieniaj pierwszej liczby. Zmień na mnożenie. Odwróć ostatnią liczbę. Albo najpierw B, potem G.
- Jeśli anulujesz obliczenia przed ich pomnożeniem, może nie być konieczne znalezienie najprostszej postaci ułamka, ponieważ wynik jest już w najprostszej postaci ułamka, jak widać. W naszym przykładzie, zanim pomnożymy 2/3 × 1/4, widzimy, że pierwszy licznik (2) i drugi mianownik (4) mają ten sam mnożnik równy 2, który możemy anulować przed kontynuowaniem obliczeń. Konwertuje to problem na 1/3 × 1/2, co daje natychmiastowy wynik 1/6 i oszczędza czas na uproszczeniu ułamka na późniejszym etapie.
- Jeśli jeden z twoich ułamków jest ujemny, ta metoda jest nadal możliwa; upewnij się, że śledzisz znaki podczas wykonywania tych kroków.
