- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:21.
- Ostatnio zmodyfikowany 2025-06-01 06:07.
Dzielenie przez liczby dziesiętne wydaje się początkowo trudne, ponieważ nikt nie nauczył cię „tabeli mnożenia 0, 7”. Sekretem tego jest przekonwertowanie problemu dzielenia na format, który używa tylko liczb całkowitych. Po przepisaniu problemu w ten sposób, stanie się on zwykłym problemem długiego dzielenia.
Krok
Część 1 z 2: Pisanie problemów jako zwykłe problemy z dzieleniem
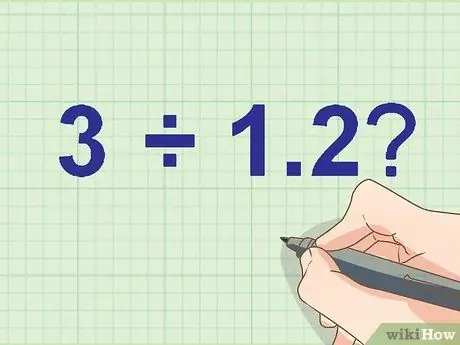
Krok 1. Zapisz swój problem z dzieleniem
Użyj ołówka, jeśli chcesz poprawić swoją pracę.
-
Przykład:
Ile 3 ÷ 1, 2?

Krok 2. Zapisz całą liczbę jako ułamek dziesiętny
Wpisz kropkę dziesiętną po liczbie całkowitej, a następnie zero po kropce dziesiętnej. Rób to, dopóki obie liczby nie będą miały tej samej wartości miejsca po prawej stronie przecinka dziesiętnego. Nie zmienia to wartości całkowitej.
-
Przykład:
W zadaniu 3 1, 2 nasza liczba całkowita to 3. Ponieważ 1, 2 ma wartość pozycyjną na prawo od przecinka, napisz 3 jako 3, 0, aby ta liczba również miała jedną wartość dziesiętną po przecinku. Teraz nasza sprawa staje się 3, 0 ÷ 1, 2.
- Uwaga: nie dodawaj zer po lewej stronie przecinka dziesiętnego! Liczba 3 jest równa 3, 0 lub 3, 00, ale nie równa się 30 lub 300.

Krok 3. Przesuń kropkę dziesiętną w prawo, aż uzyskasz liczbę całkowitą
W zadaniach dzielenia możesz przesuwać kropki dziesiętne, ale tylko wtedy, gdy przesuniesz kropki dziesiętne na wszystkich liczbach o tę samą liczbę kroków. Pozwala to przekonwertować problem na liczbę całkowitą.
-
Przykład:
Aby przekonwertować 3, 0 1, 2 na liczbę całkowitą, przesuń kropkę dziesiętną o jeden krok w prawo. Zatem 3, 0 staje się 30, a 1, 2 staje się 12. Teraz naszym problemem staje się 30 ÷ 12.

Krok 4. Napisz problem używając długiego dzielenia
Umieść podzielną liczbę (zazwyczaj większą liczbę) pod długim symbolem podziału. Wpisz numer dzielnika poza tym symbolem. Teraz masz zwykły problem z dzieleniem długim, który wykorzystuje liczby całkowite. Jeśli chcesz przypomnieć sobie, jak dzielić długie, przeczytaj następną sekcję.
Część 2 z 2: Rozwiązywanie problemów z długimi dzieleniami

Krok 1. Znajdź pierwszą cyfrę odpowiedzi
Zacznij rozwiązywać ten problem w taki sam sposób, jak zwykle, porównując dzielnik i pierwszą cyfrę dzielonej liczby. Oblicz wynik dzielenia tej pierwszej cyfry przez liczbę dzielnika, a następnie zapisz wynik powyżej tej cyfry.
Przykład: Próbujemy podzielić 30 przez 12. Porównaj 12 z pierwszą cyfrą podzielonej liczby, czyli 3. Ponieważ 12 jest większe od 3, 3 podzielone przez 12 równa się 0. Zapisz 0 powyżej 3 w wierszu odpowiedzi.
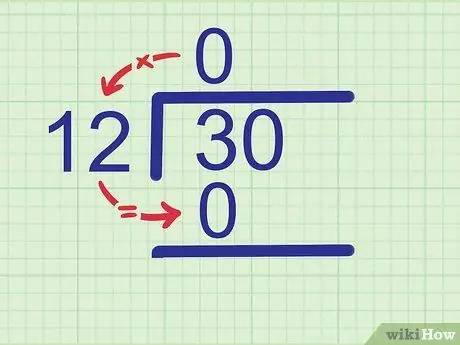
Krok 2. Pomnóż iloraz przez dzielnik
Wpisz iloczyn produktu pod podzieloną liczbą. Zapisz wynik tuż pod pierwszą cyfrą podzielonej liczby, ponieważ jest to cyfra, którą właśnie widziałeś.
-
Przykład:
Ponieważ 0 x 12 = 0, napisz 0 poniżej 3.
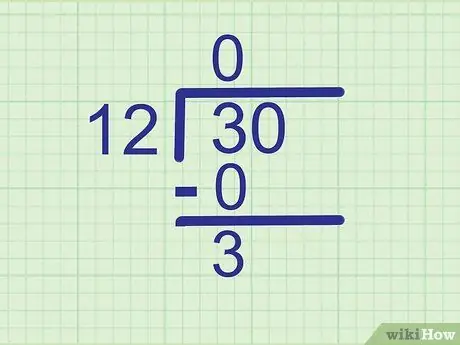
Krok 3. Odejmij, aby znaleźć resztę
Odejmij właśnie obliczony iloczyn od cyfry znajdującej się bezpośrednio nad nim. Napisz odpowiedź w nowej linii, poniżej.
-
Przykład:
3 - 0 = 3, więc napisz
Krok 3. tuż poniżej 0.
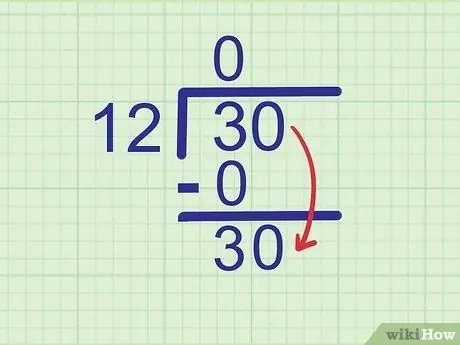
Krok 4. Obniż następną cyfrę
Upuść następną cyfrę podzielonej liczby obok liczby, którą właśnie zapisałeś.
-
Przykład:
Dzielona liczba to 30. Widzieliśmy liczbę 3, więc następną cyfrą, którą należy obniżyć, jest 0. Zmniejsz liczbę 0 do boku 3, aby stała się
Krok 30..
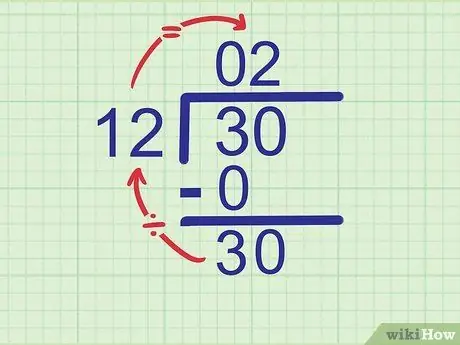
Krok 5. Spróbuj podzielić nową liczbę przez dzielnik
Teraz powtórz pierwszy krok w tej sekcji, aby znaleźć drugą cyfrę odpowiedzi. Tym razem porównaj dzielnik z liczbą, którą właśnie zapisałeś w dolnym wierszu.
-
Przykład:
Jaki jest iloraz 30 przez 12? Najbliższa odpowiedź, jaką możemy uzyskać, to 2, ponieważ 12 x 2 = 24. Napisz
Krok 2. na drugim miejscu w linii odpowiedzi.
- Jeśli nie jesteś pewien odpowiedzi, wypróbuj kilka mnożeń, aż znajdziesz największą pasującą odpowiedź. Na przykład, jeśli Twoje szacunki wynoszą 3, oblicz 12 x 3, a otrzymasz 36. Ta liczba jest za duża, ponieważ próbujemy obliczyć 30. Spróbuj obniżyć jedną liczbę, 12 x 2 = 24. Ta liczba pasuje. Zatem 2 to prawidłowa odpowiedź.

Krok 6. Powtórz powyższe kroki, aby znaleźć następny numer
Jest to ten sam proces długiego dzielenia, który zastosowano powyżej, i dla każdego problemu z długim dzieleniem:
- Pomnóż nową cyfrę odpowiedzi przez dzielnik: 2 x 12 = 24.
- Wpisz produkt w nowej linii, poniżej podzielonej liczby: Wpisz 24 tuż poniżej 30.
- Odejmij dolny wiersz od wiersza nad nim: 30 - 24 = 6. Więc wpisz 6 w nowym wierszu poniżej.

Krok 7. Kontynuuj ten proces, aż uzupełnisz ostatnią linijkę odpowiedzi
Jeśli w podzielonej liczbie nadal pozostały cyfry, obniż cyfry i kontynuuj rozwiązywanie problemu w ten sam sposób. Jeśli uzupełniłeś ostatnią linijkę odpowiedzi, przejdź do następnego kroku.
-
Przykład:
Właśnie napisaliśmy
Krok 2. w ostatniej linii odpowiedzi. Przejdź do następnego kroku.

Krok 8. W razie potrzeby dodaj ułamki dziesiętne, aby „rozszerzyć” podzieloną liczbę
Jeśli liczba jest podzielna, ostateczny wynik odejmowania wynosi „0”. Oznacza to, że zakończyłeś dzielenie i otrzymujesz odpowiedź w postaci liczby całkowitej. Jeśli jednak uzupełniłeś ostatnią linijkę odpowiedzi i nadal są cyfry, które można podzielić, musisz „rozszerzyć” liczbę podzielną, dodając kropkę dziesiętną, a następnie liczbę 0. Pamiętaj, że to nie nie zmieniaj wartości liczby.
-
Przykład:
Doszliśmy do ostatniego wiersza odpowiedzi, ale odpowiedź na nasze ostatnie odejmowanie to „6”. Wpisz „6, 0” pod symbolem długiej dzielenia, dodając „, 0” do ostatniej cyfry. Zapisz również kropkę dziesiętną w tym samym miejscu w wierszu odpowiedzi, ale nie pisz dalej.

Krok 9. Powtórz te same kroki, aby znaleźć następną cyfrę
Jedyna różnica polega na tym, że musisz dodać kropkę dziesiętną w tym samym miejscu w linii odpowiedzi. Gdy to zrobisz, możesz wyszukać pozostałe cyfry odpowiedzi w dokładnie ten sam sposób.
-
Przykład:
Upuść nowe 0 do ostatniej linii, aby stało się „60”. Ponieważ 60 podzielone przez 12 to dokładnie 5, napisz
Krok 5. jako ostatnią cyfrę naszej linii odpowiedzi. Nie zapominaj, że w naszym wierszu odpowiedzi wstawiamy przecinek dziesiętny. Więc, 2, 5 to ostateczna odpowiedź na nasze pytanie.
Porady
- Możesz zapisać to jako resztę (więc odpowiedź na 3 1, 2 to „2 pozostałe 6”). Ponieważ jednak pracujesz z ułamkami dziesiętnymi, nauczyciel może oczekiwać, że będziesz pracować z ułamkiem dziesiętnym odpowiedzi.
- Jeśli postępujesz zgodnie z metodą długiego dzielenia, zawsze będziesz mieć kropkę dziesiętną we właściwej pozycji lub w ogóle nie będziesz mieć kropki dziesiętnej, jeśli liczba jest podzielna przez podzielne. Nie próbuj zgadywać miejsc po przecinku. Miejsce dziesiętne często różni się od miejsca dziesiętnego w Twoim numerze startowym.
- Jeśli problem z długim dzieleniem nie trwa długo, możesz zatrzymać się i zaokrąglić do najbliższej liczby. Na przykład, aby rozwiązać 17 4, 2, policz do 4,047… i zaokrąglij odpowiedź do „około 4,05”.
-
Zapamiętaj warunki swojej dywizji:
- Liczba do podziału to liczba do podziału.
- Dzielnik to liczba używana do dzielenia.
- Iloraz jest odpowiedzią na problem z dzieleniem matematyki.
- Całość: podzielona przez dzielnik = iloraz.
Ostrzeżenie
Pamiętaj, że 30 12 da taką samą odpowiedź jak 3 1, 2. Nie próbuj „poprawić” swojej odpowiedzi po przesunięciu przecinka do tyłu
Powiązane artykuły wikiHow
- Zamiana wspólnych ułamków na ułamki dziesiętne
- Robienie dywizji od dawna
- Podziel ułamki przez ułamki
- Dzielenie frakcji mieszanych






