- Autor Jason Gerald [email protected].
- Public 2024-01-19 22:13.
- Ostatnio zmodyfikowany 2025-01-23 12:43.
Uczniowie, którzy są jeszcze bardzo młodzi, często mają trudności ze zrozumieniem pojęcia odejmowania. Jeśli jesteś nauczycielem i chcesz uczyć uczniów pojęcia odejmowania, spróbuj przedstawić to pojęcie w sposób interesujący i bardziej zrozumiały dla uczniów. Po wyjaśnieniu podstawowych pojęć odejmowania spróbuj przejść do pojęcia odejmowania dwucyfrowego. Gdy uczniowie opanują go dobrze, spróbuj wyjaśnić różne koncepcje, których mogą użyć do rozwiązania problemów z odejmowaniem, takich jak Common Core.
Krok
Metoda 1 z 4: Nauczanie odejmowania za pomocą obiektów lub obrazów

Krok 1. Napisz lub ustnie przedstaw uczniom problem z opowiadaniem zawierający problem odejmowania:
Na stole jest 8 pomarańczy, 3 pomarańcze zjada Jordan. Ile pomarańczy zostało?
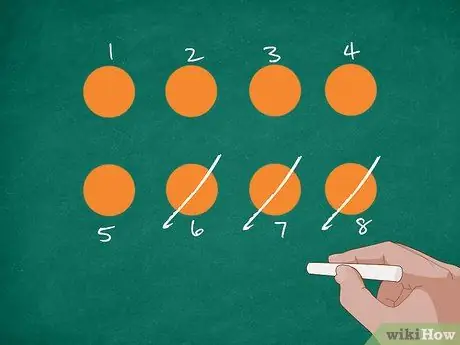
Krok 2. Przedstaw problem za pomocą zdjęć
Najpierw na tablicy lub kartce papieru narysuj 8 pomarańczowych kółek. Następnie poproś uczniów, aby policzyli liczbę i oznaczyli każdy krąg liczbą. Przekreśl 3 kółka, wyjaśniając, że Jordan zjadł 3 pomarańcze. Zapytaj uczniów, ile zostało teraz pomarańczy.
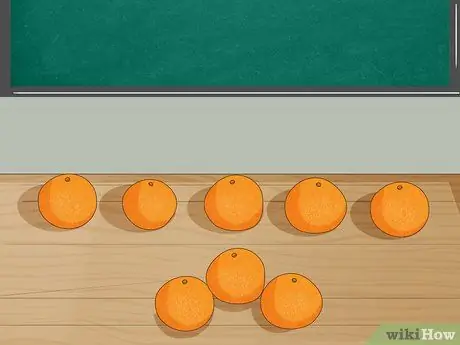
Krok 3. Przedstaw problem z obiektami
Połóż 8 pomarańczy na stole i poproś uczniów, aby policzyli liczbę. Następnie weź 3 pomarańcze ze stołu, wyjaśniając, że Jordan zjadł 3 pomarańcze. Niech uczniowie policzą liczbę pozostałych pomarańczy.

Krok 4. Zapisz równanie
Wyjaśnij, że problemy fabularne można również przedstawić za pomocą równania. Upewnij się, że zawsze prowadzisz ich w procesie przekształcania problemów fabularnych w równania matematyczne.
- Zapytaj, ile pomarańczy jest na stole. Napisz na tablicy cyfrę „8”.
- Zapytaj, ile pomarańczy zjadł Jordan. Napisz na tablicy cyfrę „3”.
- Zapytaj uczniów, czy jest to problem dodawania czy odejmowania. Wpisz znak „-” między cyframi „8” i „3”.
- Poproś uczniów, aby poszukali odpowiedzi na równanie „8-3”. Napisz znak „=”, a następnie cyfrę „5”.
Metoda 2 z 4: Nauczanie odejmowania metodą odliczania na osi liczbowej

Krok 1. Napisz lub ustnie przedstaw uczniom problem z opowiadaniem zawierający problem odejmowania:
W sklepie zoologicznym jest 10 psów, z których 6 zostało adoptowanych przez nowych właścicieli. Ile psów zostało w sklepie zoologicznym?
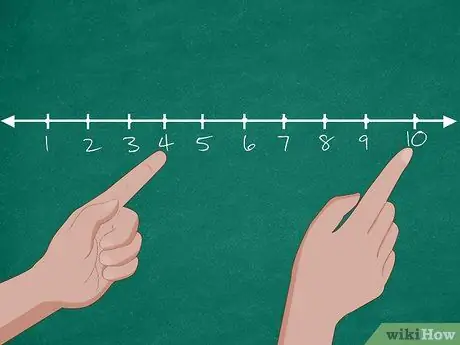
Krok 2. Użyj linii liczbowej, aby rozwiązać problem
Najpierw narysuj na tablicy linię liczbową zawierającą cyfry 0-10. Następnie poproś uczniów o podanie liczby psów w sklepie zoologicznym. Po odpowiedzi uczniów zakreśl na tablicy cyfrę „10”. Następnie zapytaj ponownie, ile psów zostało adoptowanych. Jeśli uczniowie odpowiedzą „6”, poproś ich o odliczenie 6 liczb od 10 (9, 8, 7, 6, 5, 4), aż osiągną liczbę „4”. Następnie zapytaj ponownie, ile psów zostało w sklepie zoologicznym.

Krok 3. Zapisz równanie
Wyjaśnij, że problemy fabularne można również przedstawić za pomocą równania. Upewnij się, że zawsze prowadzisz ich w procesie przekształcania problemów fabularnych w równania matematyczne.
- Zapytaj, ile psów jest w sklepie zoologicznym. Napisz na tablicy cyfrę „10”.
- Zapytaj, ile psów zostało adoptowanych. Napisz cyfrę „6” na tablicy.
- Zapytaj uczniów, czy jest to problem dodawania czy odejmowania. Wpisz znak „-” między cyframi „10” i „6”.
- Poproś uczniów, aby poszukali odpowiedzi na równanie „10-6”. Napisz znak „=”, a następnie cyfrę „4”.
Metoda 3 z 4: Nauczanie odejmowania poprzez koncepcje rodziny faktów

Krok 1. Przedstaw studentom pojęcie rodziny faktów
W rzeczywistości rodzina faktów to grupa problemów matematycznych składająca się z tych samych liczb. Na przykład liczby 10, 3 i 7 tworzą rodzinę faktów. Te trzy liczby można dodawać lub odejmować na różne sposoby; Możesz wygenerować dwa równania, używając tylko tych 3 liczb:
- 10-3=7
- 10-7=3
- 7+3=10
- 3+7=10

Krok 2. Napisz lub ustnie przedstaw uczniom problem z opowiadaniem zawierający problem odejmowania:
Mam 7 cukierków. Jeśli zjem 3 cukierki, ile cukierków zostanie?

Krok 3. Użyj koncepcji rodziny faktów, aby rozwiązać problem
Poprowadź uczniów przez proces krok po kroku:
- Zapytaj uczniów, jaki problem chcieliby rozwiązać. Napisz "7-3=?" na tablicy.
- Poproś ich, aby zidentyfikowali trzeciego członka grupy faktów. Zapisz na tablicy następujące równania: „3+_=7”; „_+3=7”; "; „7-_=3”; i 7-3=_” Następnie poproś uczniów, aby przeczytali wyniki i wypełnili problem odpowiedziami, których udzielili.
Metoda 4 z 4: Wprowadzenie wspólnych podstawowych pojęć
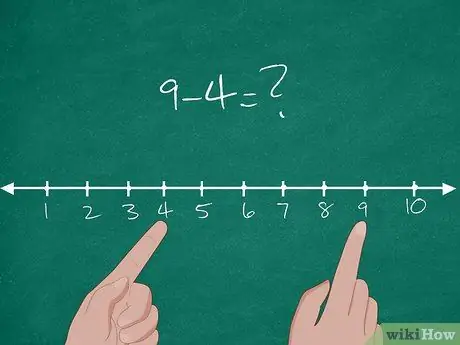
Krok 1. Naucz koncepcji odejmowania w Common Core
W rzeczywistości Common Core to nowy standard nauczania stosowany przez większość stanów w Ameryce. W Common Core podstawowa koncepcja odejmowania jest wyjaśniona odległością między dwiema liczbami. Aby wyjaśnić uczniom tę koncepcję, spróbuj narysować na tablicy oś liczbową zawierającą liczby 1-10.
- Następnie podaj uczniom podstawowy problem odejmowania: 9-4=?.
- Znajdź lokalizację cyfry 4 na osi liczbowej. Wyjaśnij uczniom, że ta lokalizacja jest ich punktem wyjścia.
- Znajdź lokalizację cyfry 9 na osi liczbowej. Wyjaśnij uczniom, że lokalizacja jest miejscem docelowym.
- Następnie poproś uczniów, aby zmierzyli lub obliczyli odległość między dwiema liczbami: „5, 6, 7, 8, 9.”.
- Odległość między tymi dwiema liczbami wynosi 5. Zatem 9-4=5.
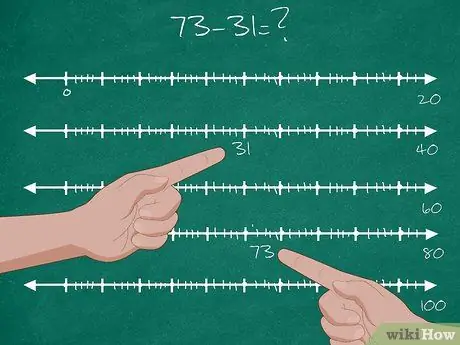
Krok 2. Niech uczniowie rozwiążą problem odejmowania dwucyfrowego
Wyjaśnij uczniom, że będą dwa punkty, w których muszą się zatrzymać przed dotarciem do celu.
- Daj uczniom dwucyfrowe zadanie odejmowania: 73-31=?.
- Znajdź lokalizację numeru 31 na osi liczbowej. To jest punkt wyjścia.
- Znajdź lokalizację numeru 73 na osi liczbowej. To jest ostateczny cel.
- „Zatrzymaj się” w pierwszej dziesiątej po 31. Zatem twój pierwszy przystanek to 40. Następnie zmierz odległość między 31 a 40 i zapisz odpowiedź: 9.
- „Zatrzymaj się” przy dziesiątych częściach, które są bliższe 73. Zatem twój drugi przystanek to 70. Następnie zmierz odległość między 40 (pierwszy przystanek) a 70 (drugi przystanek) i zapisz odpowiedź: 30.
- „Przesuń się” z 70 (drugi przystanek) do miejsca docelowego (73). Zmierz odległość między nimi i zapisz odpowiedź: 3.
- Dodaj te trzy wyniki razem: 9+30+3=42. Zatem 73-31=42.

Krok 3. Niech uczniowie rozwiążą problem odejmowania trzech cyfr
Rozwiązując zadania z odejmowaniem liczb dwucyfrowych, wyjaśnij uczniom, że zwiększy się nie tylko liczba międzylądowań, ale także odległość między poszczególnymi międzylądowaniami.
- Daj uczniom trzycyfrowe zadanie odejmowania: 815-398=?.
- Znajdź lokalizację numeru 398 na osi liczbowej. To jest punkt wyjścia.
- Znajdź lokalizację numeru 815 na osi liczbowej. To jest ostateczny cel.
- „Zatrzymaj się” w pierwszej dziesiątej po 398. Zatem twój pierwszy przystanek to 400. Zmierz odległość między 398 a 400 i zapisz odpowiedź: 2.
- "Zatrzymaj się" przy dziesiątych częściach, które są bliższe 815. Więc twój drugi przystanek to 800. Zmierz odległość między 400 a 800 i zapisz odpowiedź: 400.
- „Zatrzymaj się” przy dziesiątych częściach, które są bliższe 815. Zatem trzeci przystanek to 810. Zmierz odległość między 800 a 810 i zapisz odpowiedź: 10.
- „Przejedź” z trzeciego przystanku do miejsca docelowego, którym jest numer 815. Zmierz odległość i zapisz odpowiedź: 5.
- Dodaj wszystkie otrzymane liczby: 2+400+10+5=417. Tak więc 815-398-417.






