- Autor Jason Gerald [email protected].
- Public 2024-01-16 19:50.
- Ostatnio zmodyfikowany 2025-01-23 12:43.
W badaniu instrumentów optycznych „powiększenie” obiektu podobnego do soczewki to stosunek wysokości obrazu, który widzisz, do rzeczywistej wysokości obiektu. Na przykład obiektyw, który sprawia, że obiekt wygląda na bardzo duży, ma „wysoki” współczynnik powiększenia, podczas gdy obiektyw, który sprawia, że obiekt wygląda na mały, ma „niski” współczynnik powiększenia. Wzór na powiększenie obiektu jest zwykle obliczany za pomocą wzoru M = (hi/ho) = -(di/Do), gdzie M = powiększenie, hi = wysokość obrazu, ho = wysokość obiektu, a di i Do = odległość obrazu i przedmiotu.
Krok
Metoda 1 z 2: Obliczanie powiększenia pojedynczego obiektywu
Uwagi: A soczewka skupiająca szersze w środku niż na krawędziach (jak szkło powiększające). a soczewka rozbieżna szersze na brzegach niż w środku (jak miska). Obliczanie powiększenia na obu obiektywach jest takie samo, z jeden ważny wyjątek. Kliknij tutaj, aby przejść bezpośrednio do wyjątków dotyczących soczewek rozbieżnych.
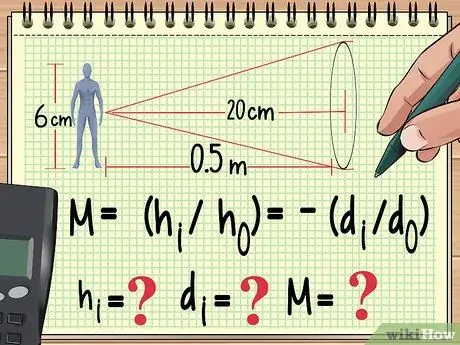
Krok 1. Zacznij od równania i zmiennych, które już znasz
Jak każdy inny problem fizyczny, sposobem na rozwiązanie problemu powiększenia jest zapisanie równania, którego użyjesz do jego obliczenia. Stąd możesz pracować wstecz, aby znaleźć wartość zmiennej, której nie znalazłeś w równaniu, którego używasz.
-
Załóżmy na przykład, że lalka o wysokości 6 cm znajduje się w odległości jednego metra od a soczewka skupiająca o ogniskowej 20 cm. Jeśli chcemy obliczyć powiększenie, wysokość obrazu i odległość obrazu, możemy zacząć pisać nasze równanie w następujący sposób:
-
- M = (hi/ho) = -(di/Do)
-
- Teraz wiemy, żeo (wysokość lalki) i do (odległość lalki od obiektywu). Znamy też ogniskową obiektywu, której nie ma w tym równaniu. Liczymy hi, Di, oraz m.

Krok 2. Użyj równania soczewki, aby uzyskać di.
Jeśli znasz odległość od obiektu, który powiększasz i ogniskową obiektywu, obliczenie odległości od tworzonego obrazu jest bardzo łatwe za pomocą równania obiektywu. Równanie soczewki to 1/f = 1/do + 1/di, gdzie f = ogniskowa obiektywu.
-
W tym przykładowym zadaniu możemy użyć równania soczewki do obliczenia di. Wprowadź wartości f i di następnie rozwiąż równanie:
-
- 1/f = 1/do + 1/di
- 1/20 = 1/50 + 1/di
- 5/100 - 2/100 = 1/di
- 3/100 = 1/di
- 100/3 = di = 33,3 cm
-
- Ogniskowa obiektywu to odległość od środka obiektywu do punktu, w którym światło przechodzi w ognisku. Jeśli kiedykolwiek skupiłeś światło za pomocą lupy na płonących mrówkach, to już to widziałeś. W pytaniach na lekcji zwykle podana jest wielkość tego punktu zapalnego. W rzeczywistości te specyfikacje są zwykle zapisane na etykiecie umieszczonej na obiektywie.

Krok 3. Obliczanie hi.
Po obliczeniu do i Di, możesz obliczyć wysokość powiększanego obiektu i powiększenie obiektywu. Zwróć uwagę na dwa znaki równości w równaniu powiększenia obiektywu (M = (hi/ho) = -(di/Do)) - oznacza to, że wszystkie części tego równania są sobie równe, więc możemy obliczyć M i hi w dowolnej kolejności.
-
Dla tego przykładowego problemu możemy obliczyć hi lubię to:
-
- (hi/ho) = -(di/Do)
- (hi/6) = -(33, 3/50)
- hi = -(33, 3/50) x 6
- hi = - 3,996 cm
-
- Zwróć uwagę, że wysokość obiektu jest tutaj ujemna, co oznacza, że obraz, który zobaczymy później, będzie odwrócony (góra-dół).

Krok 4. Obliczanie M
Możesz obliczyć ostatnią zmienną za pomocą równania -(di/Do) lub (hi/ho).
-
W poniższym przykładzie sposób obliczenia M wygląda następująco:
-
- M = (hi/ho)
- M = (-3, 996/6) = - 0, 666
-
-
Wynik będzie również taki sam, gdy zostanie obliczony przy użyciu wartości d:
-
- M = -(di/Do)
- M = -(33, 3/50) = - 0, 666
-
- Zwróć uwagę, że powiększenie nie ma etykiety jednostki.
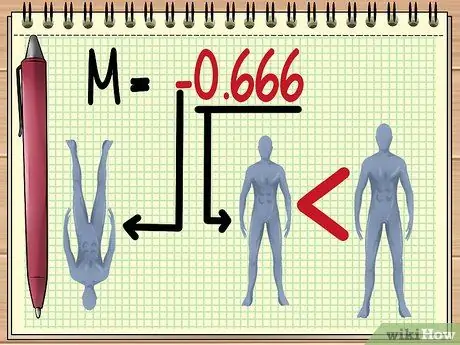
Krok 5. Zrozumienie wartości M
Gdy już uzyskasz wielkość wartości M, możesz oszacować kilka rzeczy dotyczących obrazu, który zobaczysz przez soczewkę, a mianowicie:
-
Rozmiar.
Im większa „wartość bezwzględna” M, tym większy będzie obiekt oglądany za pomocą obiektywu. Wartość M od 0 do 1 oznacza, że obiekt będzie wyglądał na mniejszy.
-
Orientacja obiektu.
Wartość ujemna oznacza, że utworzony obraz zostanie odwrócony.
- W podanym przykładzie wartość M wynosząca -0,666 oznacza, że zgodnie z wartością istniejącej zmiennej widoczny będzie cień lalki. do góry nogami i o dwie trzecie mniejsze niż rzeczywisty rozmiar.
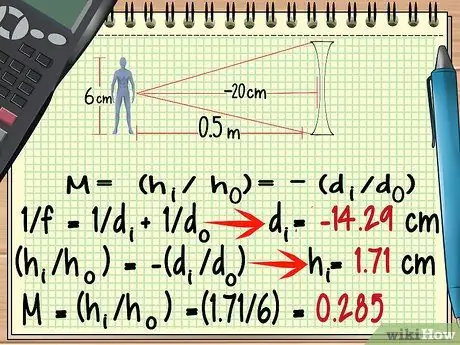
Krok 6. W przypadku soczewki rozbieżnej użyj ujemnego punktu ogniskowania
Chociaż kształt soczewki rozpraszającej bardzo różni się od kształtu soczewki skupiającej, można obliczyć jej powiększenie za pomocą tego samego wzoru, co powyżej. Wyjątki, o których należy pamiętać, to Ognisko soczewki rozpraszającej jest ujemne.
W przykładzie powyżej wpłynie to na odpowiedź, którą otrzymasz przy obliczaniu di, więc zwróć na to uwagę.
-
Przeróbmy powyższy przykładowy problem, dopiero teraz używamy obiektywu rozbieżnego z ogniskową - 20 cm.
Pozostałe zmienne pozostają niezmienione.
-
Przede wszystkim obliczymy di za pomocą równania soczewki:
-
- 1/f = 1/do + 1/di
- 1/-20 = 1/50 + 1/di
- -5/100 - 2/100 = 1/di
- -7/100 = 1/di
- -100/7 = di = - 14, 29 cm
-
-
Teraz obliczymy hi i M o wartości di nowy.
-
- (hi/ho) = -(di/Do)
- (hi/6) = -(-14, 29/50)
- hi = -(-14, 29/50) x 6
- hi = 1, 71 cm
- M = (hi/ho)
- M = (1, 71/6) = 0, 285
-
Metoda 2 z 2: Obliczanie powiększenia wielu soczewek
Prosta metoda dwóch soczewek
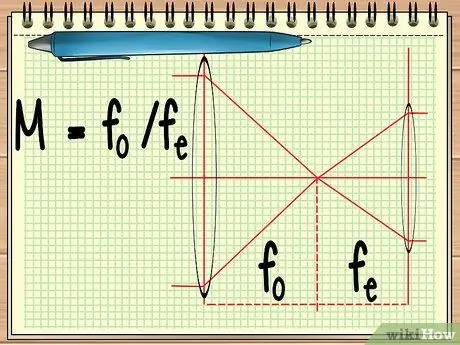
Krok 1. Oblicz ognisko dwóch soczewek
Kiedy używasz instrumentu, który składa się z dwóch soczewek ustawionych obok siebie (takich jak teleskop lub lornetka), wszystko, co musisz znaleźć, to punkt ogniskowy dwóch soczewek, aby obliczyć całkowite powiększenie obu soczewek. można to obliczyć za pomocą prostego równania M = fo/Fmi.
W równaniu fo jest ogniskiem obiektywu, a fmi jest ogniskiem okularu. Soczewka obiektywu to duża soczewka znajdująca się blisko obiektu, podczas gdy soczewka oczna to soczewka znajdująca się blisko oka obserwatora.

Krok 2. Wstaw informacje, które już posiadasz, do równania M = fo/Fmi.
Gdy masz już ogniska obu soczewek, bardzo łatwo je obliczyć, - oblicz współczynnik dzieląc ogniskową soczewki obiektywu przez ogniskową okularu. Odpowiedź, którą otrzymasz, to całkowite powiększenie narzędzia.
-
Załóżmy na przykład, że w prostym teleskopie jest napisane, że ognisko soczewki obiektywu wynosi 10 cm, a ognisko okularu 5 cm, więc powiększenie wynosi 10/5 = 2.
Skomplikowana metoda
Krok 1. Oblicz odległość między soczewkami a obiektem
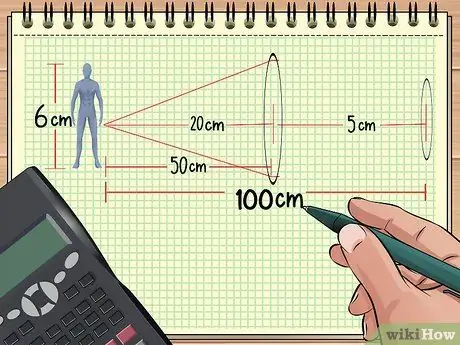
Jeśli masz dwie soczewki ustawione w rzędzie przed obiektem, całkowite powiększenie można obliczyć, jeśli znasz odległość soczewek od obiektu, rozmiar obiektu i ognisko dwóch soczewek. Pozostałą część można również obliczyć.
Załóżmy na przykład, że rozmieszczamy obiekty i soczewki tak, jak w przykładzie 1 powyżej: lalka znajduje się 50 cm od soczewki skupiającej, której ogniskowa wynosi 20 cm. Teraz umieść drugi obiektyw o ognisku 5 cm w odległości 50 cm od pierwszego obiektywu (100 cm od lalki). Następnie obliczymy całkowite powiększenie korzystając z uzyskanych informacji
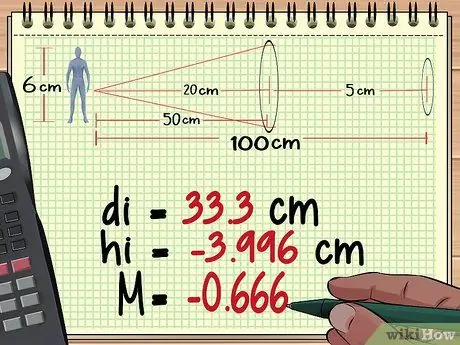
Krok 2. Oblicz odległość obiektu, wysokość i powiększenie z obiektywu 1
Pierwsza część obliczania powiększenia wielu obiektywów jest taka sama, jak obliczanie powiększenia pojedynczego obiektywu. Zacznij od obiektywu najbliżej obiektu, użyj równania obiektywu, aby znaleźć odległość od utworzonego obrazu, a następnie użyj równania powiększenia, aby znaleźć wysokość i powiększenie obrazu. Kliknij tutaj, aby wyświetlić więcej obliczeń powiększenia pojedynczego obiektywu.
-
Z naszych obliczeń w Metodzie 1 powyżej dowiadujemy się, że pierwsza soczewka daje obraz tak wysoki, jak - 3,996 cm, dystans 33,3 cm za obiektywem i przy powiększeniu - 0, 666.
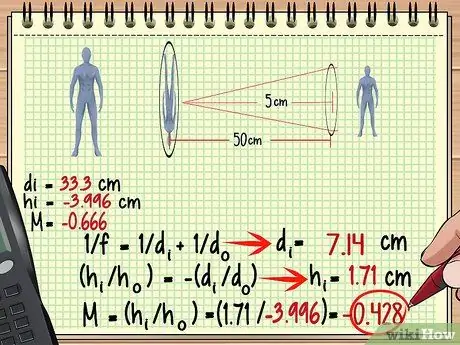
Krok 3. Użyj obrazu z pierwszej soczewki jako obiektu z drugiej soczewki
Teraz znalezienie powiększenia, wysokości i więcej dla drugiego obiektywu jest bardzo łatwe - po prostu użyj tej samej metody, której użyłeś dla pierwszego obiektywu, tylko tym razem potraktuj obraz jako obiekt. Pamiętaj, że odległość obrazu do drugiej soczewki nie zawsze jest taka sama jak odległość obiektu do pierwszej soczewki.
-
W powyższym przykładzie, ponieważ obraz powstaje 33,3 cm za pierwszą soczewką, odległość wynosi 50-33,3 = 16,7 cm przed drugim obiektywem. Wykorzystajmy ten pomiar i ogniskową drugiej soczewki, aby znaleźć obraz utworzony przez drugą soczewkę.
-
- 1/f = 1/do + 1/di
- 1/5 = 1/16, 7 + 1/di
- 0, 2 - 0,0599 = 1/di
- 0, 14 = 1/di
- Di = 7, 14 cm
-
-
Teraz możemy obliczyć hi i M dla drugiego obiektywu:
-
- (hi/ho) = -(di/Do)
- (hi/-3, 996) = -(7, 14/16, 7)
- hi = -(0, 427) x -3, 996
- hi = 1, 71 cm
- M = (hi/ho)
- M = (1, 71/-3, 996) = - 0, 428
-
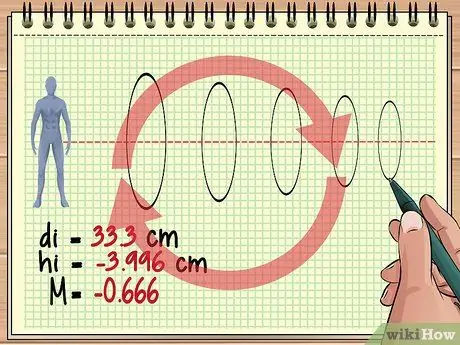
Krok 4. Kontynuuj obliczenia w ten sposób dla dodatkowych soczewek
To podstawowe podejście jest takie samo, jeśli przed obiektem znajdują się trzy, cztery lub setki soczewek. Dla każdego obiektywu rozważ obraz poprzedniego obiektywu jako obiekt i użyj równania obiektywu i równania powiększenia, aby znaleźć odpowiedź, której potrzebujesz.
Należy pamiętać, że każda kolejna soczewka może w sposób ciągły odwracać utworzony obraz. Na przykład uzyskana wcześniej wartość powiększenia (-0, 428) wskazuje, że obraz, który zobaczymy, jest w przybliżeniu 4/10 rzeczywistego rozmiaru obiektu, ale prostopadły, ponieważ obraz z poprzedniego obiektywu jest odwrócony
Porady
- Lornetki zwykle zawierają wyjaśnienie specyfikacji powiększenia w postaci liczby razy innej liczby. Na przykład lornetki można określić jako 8x25 lub 8x40. Tak napisana pierwsza liczba to powiększenie lornetki. Nie ma znaczenia, że w podanym przykładzie obie liczby różnią się wielkością, obie lornetki mają powiększenie 8-krotne. Druga liczba wskazuje, jak wyraźny obraz będzie tworzony przez lornetkę.
- Pamiętaj, że w przypadku lup jednoobiektywowych powiększenie będzie ujemne, jeśli odległość obiektu jest większa niż ogniskowa obiektywu. Nie oznacza to, że powstały obraz będzie mniejszy. W takim przypadku powiększenie nadal występuje, ale utworzony obraz będzie widziany przez obserwatora do góry nogami (top-down).






