Jak obliczyć średnią prędkość: 12 kroków (ze zdjęciami)

2024 Autor: Jason Gerald | [email protected]. Ostatnio zmodyfikowany: 2024-02-01 14:15

Wszystko, czego potrzebujesz, aby obliczyć średnią prędkość, to całkowite przemieszczenie. lub zmiana pozycji i całkowity czas. Pamiętaj, że prędkość oblicza również kierunek i prędkość obiektu, więc w odpowiedzi podaj kierunek, na przykład „północ”, „przód” lub „w lewo”. Jeśli Twój problem z obliczaniem prędkości obejmuje również stałe przyspieszenie, możesz nauczyć się szybkiego sposobu na znalezienie odpowiedzi jeszcze łatwiej.

Krok

Metoda 1 z 2: Obliczanie średniej prędkości przemieszczenia i czasu

Krok 1. Pamiętaj, że prędkość obejmuje zarówno prędkość, jak i kierunek obiektu

Prędkość opisuje szybkość, z jaką zmienia się pozycja obiektu. Ma to związek nie tylko z szybkością poruszania się obiektu, ale także z jego kierunkiem. „100 metrów na sekundę na południe” to inna wartość prędkości niż „100 metrów na sekundę na wschód”.

Wielkości, które mają kierunek, nazywane są wielkościami wektorowymi”. Wielkość tę można odróżnić od wielkości bezkierunkowej zwanej wielkością skalarną, pisząc strzałkę nad zmienną. Na przykład zapis v reprezentuje tempo, podczas gdy zapis v ^→ reprezentuje prędkość lub prędkość + kierunek. Notacja v użyta w tym artykule reprezentuje szybkość.
W problemach naukowych do wyrażania odległości należy używać metrów lub innych jednostek metrycznych, natomiast do celów codziennych można używać dowolnej jednostki.

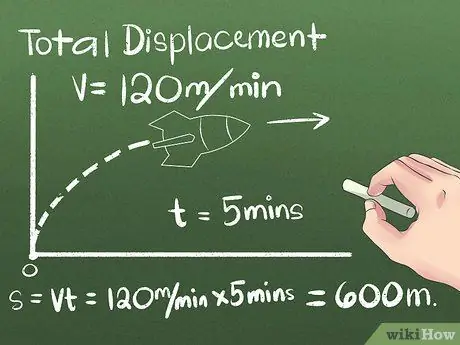
Krok 2. Znajdź całkowitą wartość przemieszczenia

Przemieszczenie to zmiana pozycji obiektu lub odległości i kierunku między jego punktem początkowym i końcowym. Kierunek, w którym porusza się obiekt przed osiągnięciem ostatecznej pozycji, można pominąć, ponieważ brana jest pod uwagę tylko odległość między punktem początkowym i końcowym. W pierwszym przykładzie użyjemy obiektu poruszającego się ze stałą prędkością w jednym kierunku:

Powiedzmy, że rakieta leci na północ przez 5 minut ze stałą prędkością 120 metrów na minutę. Aby obliczyć końcową pozycję, użyj wzoru s = vt lub użyj praktycznego myślenia, aby obliczyć odległość przebytą przez rakietę po tym (5 minut) (120 metrów/minutę) = 600 metrów na północ od punktu wyjścia.
W przypadku problemów związanych ze stałym przyspieszeniem można je rozwiązać za pomocą s = vt + at²lub użyj krótkiej metody opisanej w innej sekcji, aby znaleźć odpowiedź.

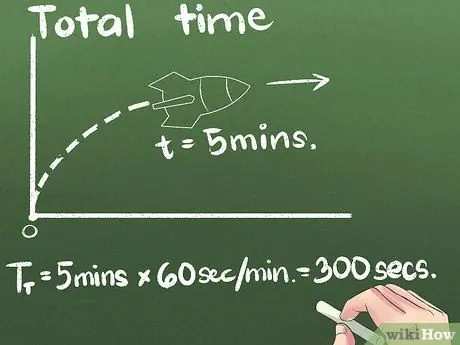
Krok 3. Znajdź całkowity czas spędzony

W naszym przykładzie rakieta porusza się do przodu przez 5 minut. Możesz wyrazić średnią prędkość w dowolnej jednostce czasu, ale druga to międzynarodowa naukowa jednostka standardowa. W tym przykładzie zmienimy jednostki sekund: (5 minut) x (60 sekund/minutę) = 300 sekund.

Nawet w problemach naukowych, jeśli pytanie dotyczy godziny lub większej jednostki czasu, łatwiej będzie najpierw obliczyć prędkość, a następnie przeliczyć ostateczną odpowiedź na metry/sekundę

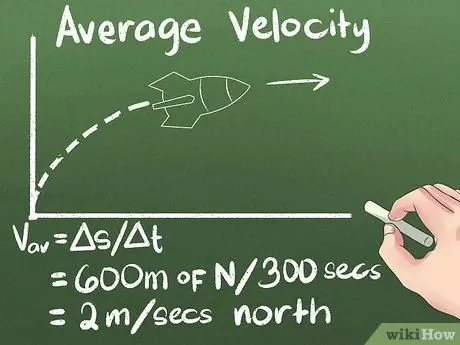
Krok 4. Oblicz średnią prędkość jako przemieszczenie w czasie

Jeśli wiesz, jak daleko porusza się obiekt i ile czasu zajmie mu dotarcie tam, będziesz wiedział, jak szybko się porusza. Tak więc dla przykładu, którego używamy, średnia prędkość rakiety wynosi (600 metrów na północ) / (300 sekund) = 2 metry/sekunda północ.

Pamiętaj o podaniu kierunku (np. „przód” lub „północ”).
W formule v_av = s/Δt. Symbol delta oznacza „zmianę”, więc s/Δt oznacza „zmianę pozycji w czasie”.
Średnia prędkość może być zapisana jako v_avlub jako v z poziomą linią nad nim.

Krok 5. Rozwiąż bardziej skomplikowane problemy

Jeśli obiekt zmieni kierunek lub prędkość, nie daj się zmylić. Średnia prędkość jest nadal „jedynie” obliczana na podstawie całkowitego przemieszczenia i całkowitego czasu. To, co dzieje się między punktem początkowym a końcowym, możesz zignorować. Oto kilka przykładów obiektu podróżującego z tym samym przemieszczeniem i całkowitym czasem, a więc z tą samą średnią prędkością:

Anna idzie na zachód z prędkością 1 metra/s przez 2 sekundy, po czym nagle przyspiesza do 3 metrów/sekundę i kontynuuje marsz na zachód przez 2 sekundy. Całkowite przemieszczenie wynosi (1 m/s na zachód) (2 s) + (3 m/s na zachód) (2 s) = 8 metrów na zachód. Całkowity czas wynosi 2 sekundy + 2 sekundy = 4 sekundy. Tak więc średnia prędkość wynosi 8 metrów na zachód/4 sekundy = 2 metry/sekundę na zachód.
Bart idzie na zachód z prędkością 5 m/s przez 3 sekundy, potem odwraca się i idzie na wschód z prędkością 7 m/s przez 1 sekundę. Możemy myśleć o ruchu na wschód jako o „ujemnym ruchu na zachód”, więc całkowite przemieszczenie wynosi = (5 metrów/s na zachód)(3 s) + (-7 m/s na zachód)(1 s) = 8 metrów. Całkowity czas = 4 sekundy. Średnia prędkość = 8 metrów na zachód / 4 sekundy = 2 metry/sekundę na zachód.
Charlotte przeszła 1 metr na północ, a następnie 8 metrów na zachód, a następnie 1 metr na południe. Czas potrzebny na ukończenie całej podróży to 4 sekundy. Narysuj diagram na kartce papieru, a zobaczysz, że punkt końcowy znajduje się 8 metrów na zachód od punktu początkowego, więc ta wartość to przemieszczenie. Całkowity czas to 4 sekundy, więc średnia prędkość to 8 metrów na zachód / 4 sekundy = 2 metry/sekundę na zachód.

Metoda 2 z 2: Obliczanie średniej prędkości stałego przyspieszenia

Krok 1. Rozważ prędkość początkową i stałe przyspieszenie

Powiedzmy, że naszym problemem jest „Rower porusza się w prawo z prędkością 5 m/s, ze stałym przyspieszeniem 2 m/s². Jeśli ten rower porusza się przez 5 sekund, jaka jest jego średnia prędkość?”

Jeśli jednostka „metr/sekunda”²„ aby cię zmylić, zapisz to jako „metry/sekundę/sekundę” lub „metry na sekundę na sekundę”. Przyspieszenie 2 metry/sekundę/sekundę oznacza, że prędkość wzrasta o 2 metry na sekundę na sekundę.

Krok 2. Użyj przyspieszenia, aby znaleźć prędkość końcową

Przyspieszenie, oznaczone zapisem a, jest szybkością zmiany prędkości (lub szybkości). Prędkość wzrasta w stałym tempie wzrostu. Możesz narysować tabelę za pomocą przyspieszenia, aby znaleźć prędkość w różnych momentach podczas podróży rowerem. Musimy utworzyć tę tabelę, aby znaleźć punkt końcowy problemu (w t = 5 sekund), ale stworzymy dłuższą tabelę, aby ułatwić zrozumienie tej koncepcji:

W punkcie startowym (czas t = 0 sekund) rower porusza się z prędkością 5 metrów/s.
Po 1 sekundzie (t = 1) rower porusza się z prędkością 5 metrów/sekundę + z prędkością = 5 metrów/sekundę + (2 metry/sekundę²)(1 sekunda) = 7 metrów/sekundę.
W t = 2 rower porusza się w prawo z prędkością 5+(2)(2) = 9 metrów/sek.
W t = 3 rower porusza się w prawo z prędkością 5+(2)(3) = 11 metrów/s.
W t = 4 rower porusza się w prawo z prędkością 5+(2)(4) = 13 metrów/sek.
W t = 5 rower porusza się w prawo z prędkością 5+(2)(5) = 15 metrów/sekundę.

Krok 3. Użyj tego wzoru, aby znaleźć średnią prędkość

Jeśli i „tylko”, jeśli przyspieszenie jest stałe, średnia prędkość będzie równa średniej wartości sumy prędkości końcowej i początkowej. (v_F +v_i)/2. Dla naszego przykładowego problemu powyżej, początkowa prędkość roweru wynosi v_i 5 metrów/sekundę. Po obliczeniu prędkość końcowa wynosi v_F 15 metrów/sekundę. Dodając te dwie wartości razem otrzymujemy (15 metrów/sekundę + 5 metrów/sekundę) / 2 = (20 metrów/sekundę) / 2 = 10 metrów/sekundę w prawym kierunku.

Pamiętaj, aby podać kierunek, w tym przypadku „właściwy”.
Termin ten można zapisać jako v₀ (prędkość w czasie 0 lub prędkość początkowa) i v (prędkość końcowa).

Krok 4. Zrozum intuicyjnie wzór na średnią prędkość

Aby znaleźć średnią prędkość, możemy użyć prędkości w dowolnym punkcie i znaleźć średnią dla nich wszystkich. (Jest to definicja średniej.) Ponieważ wymaga to rachunku różniczkowego lub nieskończonego czasu, zrozum ten wzór bardziej intuicyjnie. Zamiast brać za każdym razem, oblicz średnią prędkość dwóch punktów czasowych i zobacz wyniki. Jeden punkt w czasie jest w pobliżu początku jazdy, gdzie rower jedzie powoli, a inny punkt jest w pobliżu punktu końcowego, w którym rower jedzie szybko.

Krok 5. Przetestuj teorię intuicyjną

Skorzystaj z powyższej tabeli, aby określić prędkość w różnych punktach w czasie. Niektóre pary spełniające nasze kryteria to (t=0, t=5), (t=1, t=4) lub (t=2, t=3). Możesz przetestować tę formułę z wartościami t innymi niż liczby całkowite, jeśli chcesz.

Bez względu na to, którą parę punktów wybierzesz, średnia prędkość w tym czasie będzie zawsze taka sama. Na przykład ((5+15)/2), ((7+13)/2) lub ((9+11)/2) wszystkie równają się 10 m/s w prawo

Krok 6. Uzupełnij intuicyjne wyjaśnienie

Jeśli użyjemy tej metody z listą każdorazowo pobranych czasów, będziemy nadal obliczać średnią z pierwszej połowy podróży i drugiej połowy podróży. Czas potrzebny na pokonanie każdej połowy jest taki sam, więc nie tracimy prędkości, gdy kończymy liczenie.

Ponieważ każda para da ten sam wynik, średnia z tych prędkości również będzie miała taką samą wartość. W naszym przykładzie prędkość całości wynosi „10 metrów/s w prawo” i nadal będzie wynosić 10 metrów/s w prawo.
Możemy znaleźć tę wartość, obliczając średnią dowolnej pary, na przykład prędkość początkową i końcową. W naszym przykładzie prędkości te są osiągane przy t=0 it=5 i można je obliczyć za pomocą powyższego wzoru: (5+15)/2 = 10 metrów/s w prawo.

Krok 7. Zrozum tę formułę matematycznie

Jeśli czujesz się bardziej komfortowo z dowodami spisanymi jako formuły, możesz zacząć od wzoru, aby obliczyć przebytą odległość przy założeniu stałego przyspieszenia i wyprowadzić z tego wzór:

s = v_it + w². (Technicznie s i t lub zmiana pozycji i zmiana w czasie, ale zostaniesz również zrozumiany, jeśli napiszesz s i t.)
Średnia prędkość v_av zdefiniowany jako s/t, więc formułę wpisujemy w postaci s/t.
v_av = s/t = v_i + w
Przyspieszenie x czas jest równe zmianie całkowitej prędkości lub v_F - v_i. Możemy więc zastąpić „at” w formule i uzyskać:
v_av = v_i + (v_F - v_i).
Uprość: v_av = v_i + v_F - v_i = v_i + v_F = (v_F +v_i)/2.

Porady

Prędkość różni się od prędkości, ponieważ prędkość jest wielkością wektorową, podczas gdy prędkość jest wielkością skalarną. Ilości wektorowe obejmują zarówno kierunek, jak i wielkość, podczas gdy wielkości skalarne obejmują tylko wielkość.
Jeśli obiekt porusza się w jednym wymiarze, na przykład lewo-prawo, możesz użyć liczby dodatniej, aby przedstawić jeden kierunek (na przykład w prawo), a liczby ujemnej, aby przedstawić inny kierunek (w lewo). Zapisz tę notację u góry strony, aby była jasna dla osób czytających Twoją pracę.