Dzięki współczynnikowi korelacji rang Spearmana możemy określić, czy dwie zmienne mają zależność funkcji monotonicznej (to znaczy, gdy jedna liczba wzrośnie, druga również wzrośnie lub odwrotnie). Aby obliczyć współczynnik korelacji rang Spearmana, musisz uszeregować i porównać zestawy danych, aby znaleźć d2, a następnie wprowadź dane do standardowej lub uproszczonej formuły współczynnika korelacji rang Spearmana. Możesz również obliczyć te współczynniki za pomocą formuł programu Excel lub polecenia R.
Krok
Metoda 1 z 3: sposób ręczny
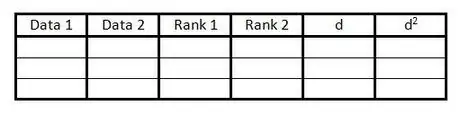
Krok 1. Utwórz tabelę
Tabela zawiera wszystkie informacje potrzebne do obliczenia współczynnika korelacji rang Spearmana. Potrzebujesz takiego stołu:
- Utwórz 6 kolumn z nagłówkami, jak w przykładzie.
- Przygotuj tyle pustych wierszy, ile jest par danych.
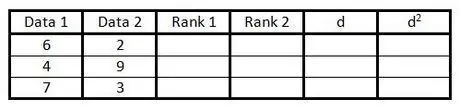
Krok 2. Wypełnij pierwsze dwie kolumny parami danych
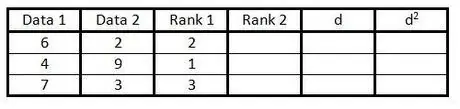
Krok 3. Wprowadź ranking pierwszej kolumny grup danych w trzeciej kolumnie od 1 do n (liczba danych)
Przyznaj ocenę 1 za najniższą wartość, ocenę 2 za następną najniższą wartość i tak dalej.
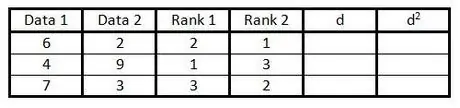
Krok 4. W czwartej kolumnie wykonaj to samo, co w kroku 3, ale uszereguj dane w drugiej kolumnie
-
Średnia_742 Jeśli istnieją dwa (lub więcej) dane o tej samej wartości, oblicz średnią ocenę danych, a następnie wprowadź ją do tabeli na podstawie tej średniej wartości.
W przykładzie po prawej stronie są dwie wartości 5 na ocenach 2 i 3. Ponieważ są dwie piątki, znajdź średnią ocen. Średnia 2 i 3 to 2,5, więc wprowadź wartość oceny 2,5 dla obu wartości 5.
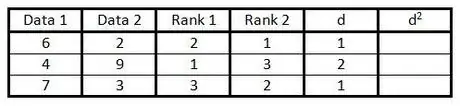
Krok 5. W kolumnie „d” oblicz różnicę między dwiema liczbami w kolumnie rang
Oznacza to, że jeśli jedna kolumna ma rangę 1, a druga 3, różnica wynosi 2. (Znak nie ma znaczenia, ponieważ następnym krokiem jest podniesienie wartości do kwadratu).
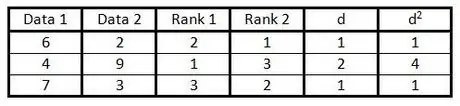
Krok 6. Podnieś każdą liczbę do kwadratu w kolumnie „d” i wpisz wynik w kolumnie „d2".
Krok 7. Dodaj wszystkie dane w kolumnie „d2".
Wynik to d2.
Krok 8. Wybierz jedną z następujących formuł:
-
Jeśli żadna z ocen nie jest taka sama jak w poprzednim kroku, wprowadź tę wartość w uproszczonym wzorze współczynnika korelacji rang Spearmana
Krok 8_271 i zamień "n" na liczbę par danych, aby uzyskać wynik.
Krok 9_402 -
Jeśli w poprzednim kroku istnieje podobna ranga, użyj standardowego wzoru na współczynnik korelacji rang Spearmana:
Spearman
Krok 9. Zinterpretuj wyniki
Wartość może wahać się od -1 do 1.
- Jeśli wartość jest bliska -1, korelacja jest ujemna.
- Jeśli wartość jest bliska 0, nie ma korelacji liniowej.
- Jeśli wartość jest bliska 1, korelacja jest dodatnia.
Metoda 2 z 3: Korzystanie z programu Excel
Krok 1. Utwórz nową kolumnę dla danych wraz z ich rankingiem
Na przykład, jeśli Twoje dane znajdują się w kolumnie A2:A11, użyj formuły „=RANK(A2, A2:A$11)” i skopiuj ją w dół, aż pokryje wszystkie kolumny i wiersze.
Krok 2. Zmień tę samą ocenę, jak opisano w krokach 3 i 4 metody 1
Krok 3. W nowej komórce oblicz korelację między dwiema kolumnami rang za pomocą formuły „=CORREL(C2:C11, D2:D11)”
W tym przykładzie litery C i D odnoszą się do kolumny, w której znajduje się ranking. Nowa komórka zostanie wypełniona korelacją rang włóczników.
Metoda 3 z 3: Korzystanie z R
Krok 1. Najpierw zainstaluj program R, jeśli jeszcze go nie masz
(Patrz
Krok 2. Zapisz swoje dane w formie CSV, umieść dane, które chcesz znaleźć korelację w pierwszych dwóch kolumnach
Możemy to zrobić za pomocą menu „Zapisz jako”.
Krok 3. Otwórz Edytor R
Jeśli pracujesz z terminala, po prostu uruchom R. Jeśli pracujesz z pulpitu, kliknij ikonę R.
Krok 4. Wpisz następujące polecenie:
- d <- read.csv("NAZWA_TWOJEGO_CSV.csv") i naciśnij klawisz Enter.
- cast(ranga(d[, 1]), rank(d[, 2]))
Porady
Dane muszą składać się z co najmniej 5 par, aby można było zobaczyć trend (liczba danych w przykładzie to 3 pary tylko w celu uproszczenia obliczeń)
Ostrzeżenie
- Współczynnik korelacji rang Spearmana określa siłę korelacji tylko wtedy, gdy dane stale rosną lub spadają. Jeśli istnieje inny trend w danych, korelacja rang Spearmana nie zapewni dokładną reprezentację.
- Ta formuła opiera się na założeniu, że nie ma równych ocen. Gdy jest taka sama ranga jak w przykładzie, powinniśmy użyć tej definicji: współczynnik korelacji momentu mnożenia przez rangę.
