- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:21.
- Ostatnio zmodyfikowany 2025-06-01 06:07.
Siła normalna to wielkość siły wymaganej do zanegowania innych sił w dowolnym scenariuszu. Najlepszy sposób na znalezienie tego zależy od stanu obiektu i posiadanych zmiennych. Czytaj dalej, aby dowiedzieć się więcej.
Krok
Metoda 1 z 5: Normalny styl w spoczynku
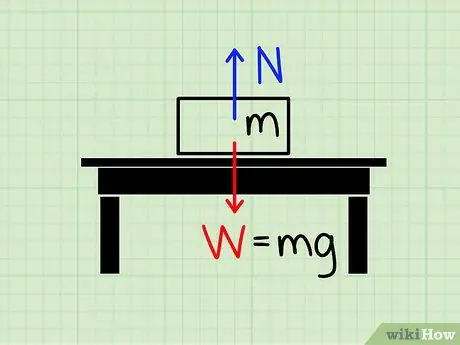
Krok 1. Zrozum znaczenie siły normalnej
Siła normalna odnosi się do wielkości siły użytej do zanegowania siły grawitacyjnej.
Wyobraź sobie blok leżący na stole. Siła grawitacji ciągnie klocek w kierunku ziemi, ale wyraźnie działa siła, która uniemożliwia klocowi zmiażdżenie stołu i upadek na ziemię. Siła, która działa, aby zatrzymać ten blok pomimo siły grawitacji, nazywa się normalny styl.
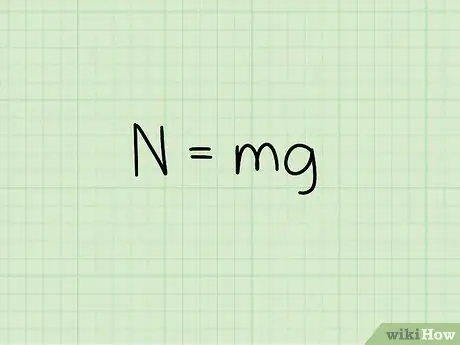
Krok 2. Poznaj równanie siły normalnej działającej na obiekt w spoczynku
Obliczając siłę normalną obiektu, gdy spoczywa on na płaskiej powierzchni, użyj wzoru: N = m * g
- W tym równaniu n symbolizują normalny styl, m reprezentuje masę obiektu, a g reprezentuje przyspieszenie ziemskie.
- W przypadku przedmiotu, który znajduje się w spoczynku na płaskiej powierzchni, bez działającej siły zewnętrznej, siła normalna jest równa ciężarowi przedmiotu. Aby utrzymać obiekt w spoczynku, siła normalna musi być równa sile grawitacji działającej na obiekt. Siła grawitacyjna działająca na obiekt to ciężar obiektu lub masa obiektu pomnożona przez przyspieszenie grawitacyjne.
- Przykład: Znajdź siłę normalną bloku o masie 4,2 kg.
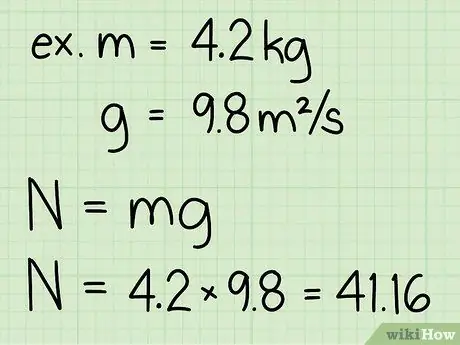
Krok 3. Pomnóż masę obiektu i przyspieszenie grawitacyjne
To pomnożenie da ciężar obiektu, który oczywiście jest równy normalnej sile ciała w spoczynku.
- Zauważ, że przyspieszenie grawitacyjne na powierzchni Ziemi jest zawsze stałe: g = 9,8 m/s2
- Przykład: waga = m * g = 4, 2 * 9, 8 = 41, 16

Krok 4. Zapisz swoje odpowiedzi
Poprzedni krok rozwiąże problem, dając ci odpowiedź.
Przykład: Siła normalna to 41, 16 N
Metoda 2 z 5: Siła normalna na pochyłej płaszczyźnie
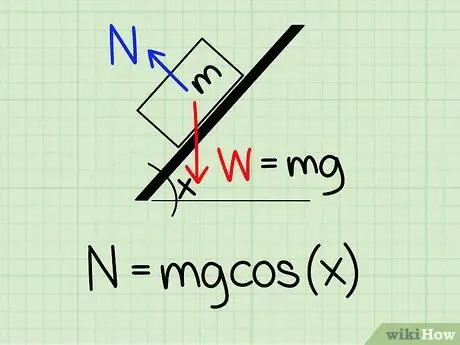
Krok 1. Użyj poprawnego równania
Aby obliczyć siłę normalną działającą na obiekt pochylony o określony kąt, musisz skorzystać ze wzoru: N = m * g * cos(x)
- Dla tego równania n symbolizują normalny styl, m reprezentuje masę obiektu g reprezentuje przyspieszenie ziemskie, a x reprezentuje kąt skośny.
- Przykład: Znajdź siłę normalną bloku o masie 4,2 kg, który spoczywa na płaszczyźnie nachylonej pod kątem 45 stopni.

Krok 2. Znajdź cosinus kąta
Cosinus kąta jest równy sinusowi kąta dopełniającego lub przyległego boku podzielonego przez przeciwprostokątną trójkąta utworzonego przez nachylenie.
- Wartość tę często określa się za pomocą kalkulatora, ponieważ cosinus dowolnego kąta jest zawsze stały, ale można go również obliczyć ręcznie.
- Przykład: cos(45) = 0,71
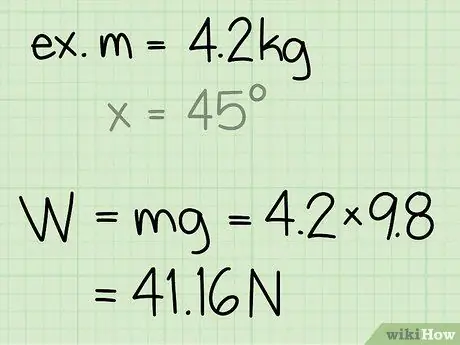
Krok 3. Znajdź wagę przedmiotu
Masa obiektu jest równa masie obiektu pomnożonej przez przyspieszenie ziemskie.
- Zauważ, że przyspieszenie grawitacyjne na powierzchni Ziemi jest zawsze stałe: g = 9,8 m/s2
- Przykład: waga = m * g = 4, 2 * 9, 8 = 41, 16
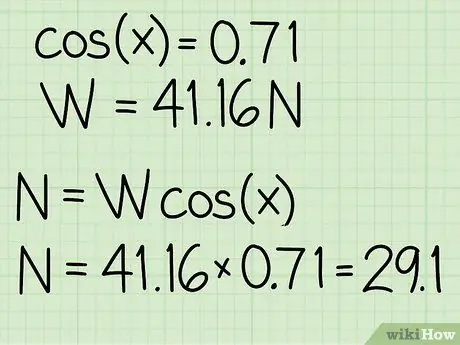
Krok 4. Pomnóż dwie wartości
Aby znaleźć siłę normalną, musisz pomnożyć ciężar przedmiotu przez cosinus kąta nachylenia.
Przykład: N = m * g * cos(x) = 41, 16 * 0, 71 = 29, 1
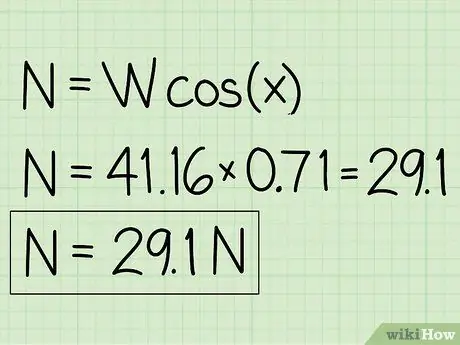
Krok 5. Zapisz swoje odpowiedzi
Poprzedni krok rozwiąże problem i udzieli odpowiedzi.
- Zwróć uwagę, że gdy obiekt jest w spoczynku na pochyłości, siła normalna będzie mniejsza niż ciężar obiektu.
- Przykład: Siła normalna wynosi 29,1 N.
Metoda 3 z 5: Normalny styl z zewnętrznym stylem puchu
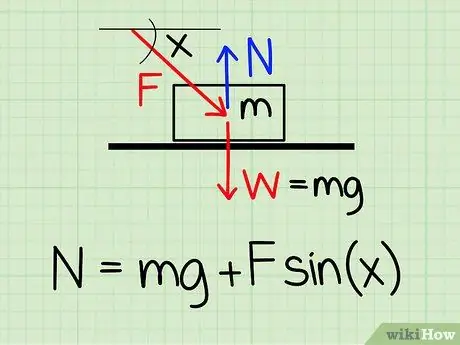
Krok 1. Użyj poprawnego równania
Aby obliczyć siłę normalną działającą na obiekt w spoczynku, jeśli na obiekt działa zewnętrzna siła skierowana w dół, użyj równania: N = m * g + F * sin(x)'
- n symbolizują normalny styl, m reprezentuje masę obiektu g reprezentuje przyspieszenie ziemskie, F symbolizuje styl zewnętrzny i x reprezentuje kąt między obiektem a kierunkiem siły zewnętrznej.
- Przykład: Znajdź siłę normalną obiektu o masie 4,2 kg, jeśli obiekt jest popychany przez osobę pod kątem 30 stopni i siłą 20,9 N.
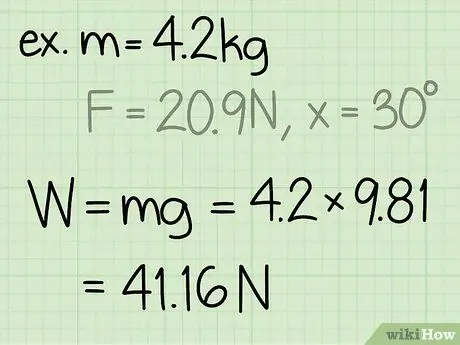
Krok 2. Znajdź wagę przedmiotu
Masa obiektu jest równa masie obiektu pomnożonej przez przyspieszenie ziemskie.
- Zauważ, że przyspieszenie grawitacyjne na powierzchni Ziemi jest zawsze stałe: g = 9,8 m/s2
- Przykład: waga = m * g = 4, 2 * 9, 8 = 41, 16
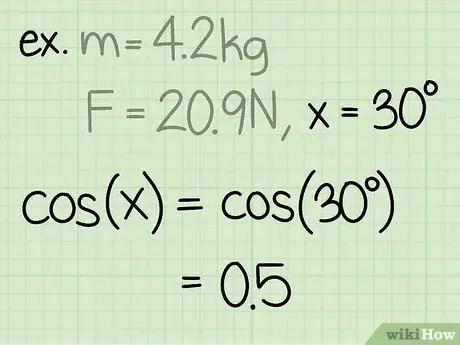
Krok 3. Znajdź sinus kąta
Sinus kąta jest obliczany przez podzielenie boku trójkąta przeciwległego do kąta przez przeciwprostokątną kąta.
Przykład: grzech (30) = 0,5

Krok 4. Pomnóż sinus przez siłę zewnętrzną
Siła zewnętrzna w tym przykładzie odnosi się do siły skierowanej w dół uderzającej w obiekt.
Przykład: 0, 5 * 20, 9 = 10, 45
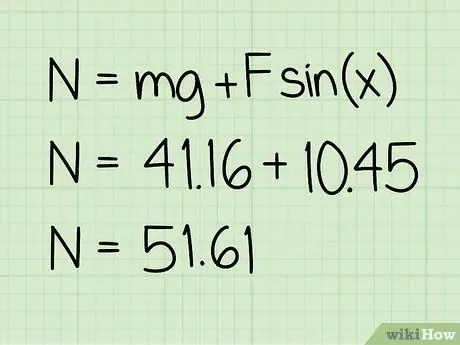
Krok 5. Dodaj tę wartość do wagi
Ta suma da wielkość działającej siły normalnej.
Przykład: 10, 45 + 41, 16 = 51, 61
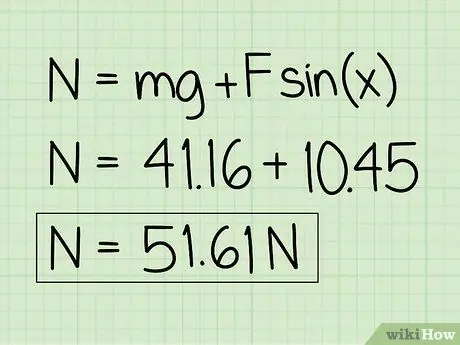
Krok 6. Zapisz swoje odpowiedzi
Zauważ, że w przypadku przedmiotu w spoczynku, na który oddziałuje zewnętrzna siła skierowana w dół, siła normalna będzie większa niż ciężar obiektu.
Przykład: Siła normalna wynosi 51,61 N
Metoda 4 z 5: Normalny styl z zewnętrznym stylem w górę
Krok 1. Użyj poprawnego równania
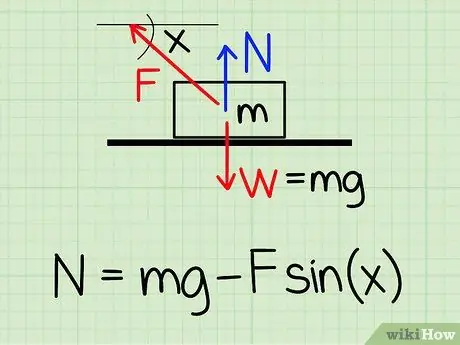
Aby obliczyć siłę normalną działającą na obiekt w spoczynku, jeśli na obiekt działa zewnętrzna siła skierowana do góry, użyj równania: N = m * g - F * sin(x)'
- n symbolizują normalny styl, m reprezentuje masę obiektu g reprezentuje przyspieszenie ziemskie, F symbolizuje styl zewnętrzny i x reprezentuje kąt między obiektem a kierunkiem siły zewnętrznej.
- Przykład: Znajdź siłę normalną klocka o masie 4,2 kg, jeśli ktoś podciągnie klocek pod kątem 50 stopni i siłą 20,9 N.

Krok 2. Znajdź wagę przedmiotu
Masa obiektu jest równa masie obiektu pomnożonej przez przyspieszenie ziemskie.
- Zauważ, że przyspieszenie grawitacyjne na powierzchni Ziemi jest zawsze stałe: g = 9,8 m/s2
- Przykład: waga = m * g = 4, 2 * 9, 8 = 41, 16
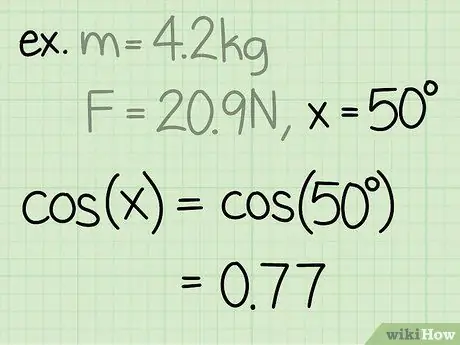
Krok 3. Znajdź sinus kąta
Sinus kąta jest obliczany przez podzielenie boku trójkąta przeciwległego do kąta przez przeciwprostokątną kąta.
Przykład: sin(50) = 0,77

Krok 4. Pomnóż sinus przez siłę zewnętrzną
Siła zewnętrzna odnosi się w tym przypadku do siły skierowanej w górę uderzającej w obiekt.
Przykład: 0,77 * 20, 9 = 16, 01
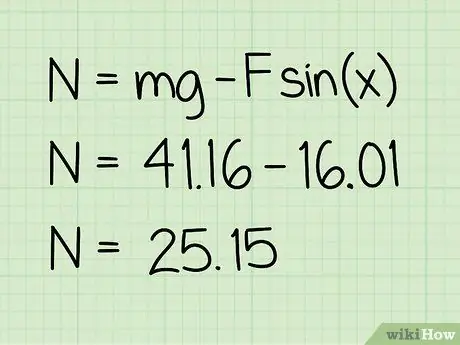
Krok 5. Odejmij tę wartość od wagi
Odejmowanie, które wykonasz, da ci wielkość działającej na nią siły normalnej.
Przykład: 41, 16 - 16, 01 = 25, 15
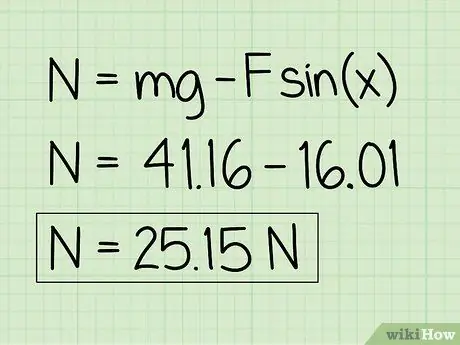
Krok 6. Zapisz swoje odpowiedzi
Zauważ, że na obiekt w spoczynku wpływa skierowana do góry siła zewnętrzna, siła normalna będzie mniejsza niż ciężar obiektu.
Przykład: Siła normalna to 25, 15 N
Metoda 5 z 5: Normalna siła i tarcie

Krok 1. Poznaj podstawowe równanie tarcia kinetycznego
Tarcie kinetyczne lub tarcie poruszającego się obiektu jest równe współczynnikowi tarcia pomnożonemu przez siłę normalną obiektu. W postaci równania: f = * N
- W tym równaniu F symbolizują tarcie, ️ reprezentuje współczynnik tarcia, a n reprezentuje normalną siłę obiektu.
- „Współczynnik tarcia” to stosunek siły tarcia do siły normalnej, która ściska dwie przeciwległe powierzchnie.
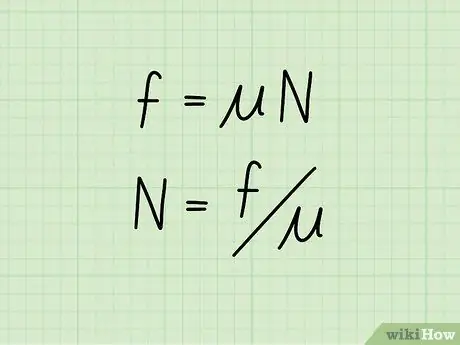
Krok 2. Ustaw równanie, aby wyizolować siłę normalną
Znając wartość tarcia kinetycznego obiektu, a także jego współczynnik tarcia, można obliczyć siłę normalną za pomocą wzoru: N = f /
- Obie strony oryginalnego równania są dzielone przez ️, izolując w ten sposób siłę normalną z jednej strony podczas obliczania współczynnika tarcia i tarcia kinetycznego z drugiej.
- Przykład: Znajdź siłę normalną bloku, jeśli współczynnik tarcia wynosi 0,4, a wielkość tarcia kinetycznego wynosi 40 N.
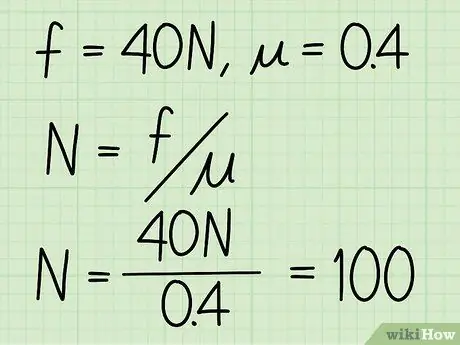
Krok 3. Podziel tarcie kinetyczne przez współczynnik tarcia
Zasadniczo to wszystko, co musisz zrobić, aby znaleźć wielkość siły normalnej.
Przykład: N = f / = 40 / 0, 4 = 100
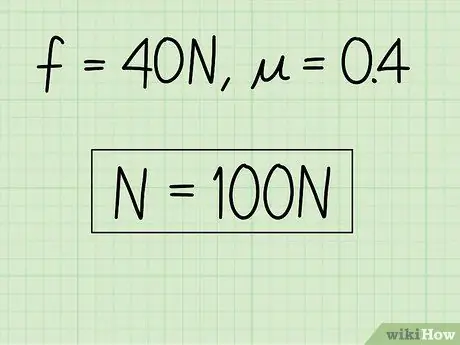
Krok 4. Zapisz swoje odpowiedzi
Jeśli chcesz, możesz sprawdzić swoją odpowiedź, podłączając ją z powrotem do oryginalnego równania tarcia kinetycznego. Jeśli tego nie chcesz, rozwiązałeś problem.






