- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:32.
- Ostatnio zmodyfikowany 2025-01-23 12:43.
Istnieje wiele różnych kształtów płaskich kształtów i istnieje wiele powodów, dla których warto obliczyć powierzchnię: od odrabiania pracy domowej po oszacowanie ilości farby potrzebnej do przemalowania salonu. Nie martw się, wikiHow ma odpowiedź! Zacznij od kroku 1 poniżej, aby dowiedzieć się, jak obliczyć powierzchnię figury samolotu.
Krok
Metoda 1 z 7: Kwadrat, prostokąt i równoległobok
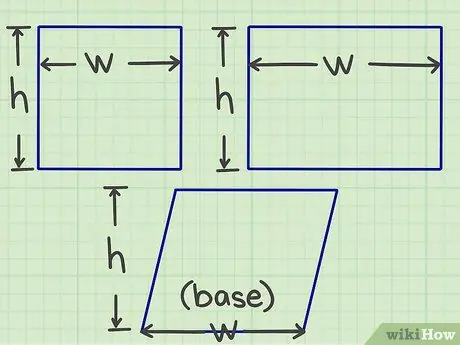
Krok 1. Zmierz długość i szerokość
Zacznij mierzyć lub obliczać długość i szerokość płaskiego kształtu (lub innymi słowy, rozmiar każdego z dwóch boków, które spotykają się w jednym punkcie).
- W przypadku równoległoboku musisz znaleźć podstawę i wysokość, ale w uproszczeniu idea jest taka sama, jak długość i szerokość.
- W prawdziwym świecie może być konieczne samodzielne zmierzenie, ale jeśli chodzi o odrabianie lekcji, nauczyciel zwykle zapisał już liczby wraz ze zdjęciem kształtu.
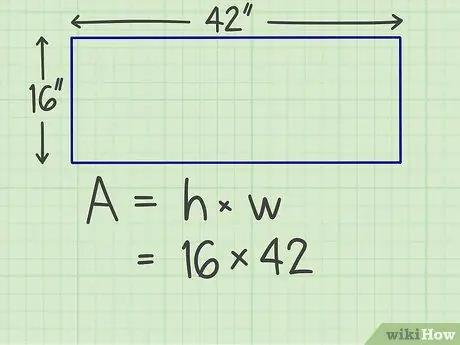
Krok 2. Pomnóż boki
Pomnóż jedną stronę przez drugą. Załóżmy na przykład, że masz prostokąt o szerokości 16 cali i długości 42 cali, więc musisz obliczyć 16 x 42.
Jeśli obliczasz powierzchnię kwadratu (dawniej kwadratu), zaoszczędź czas, ustawiając jeden z jego boków pod kwadratem za pomocą kalkulatora. Jeśli bok mierzy 4 m, naciśnij klawisz 4, a następnie naciśnij klawisz kwadratowy na kalkulatorze, aby wyświetlić wynik. Kwadrat oznacza mnożenie liczby przez siebie
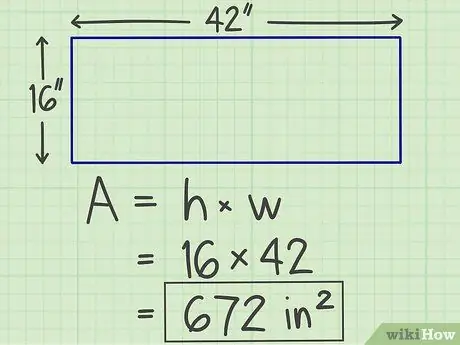
Krok 3. Zapisz wyniki
Mnożenie, które wykonałeś wcześniej, da w wyniku liczbę, czyli powierzchnię obliczonej płaszczyzny, z jednostką „kwadrat”. Tak więc obliczony wcześniej prostokąt ma powierzchnię 672 cali kwadratowych.
Czasami ta kwadratowa jednostka jest również zapisywana jako mała 2, która rośnie nieco po nazwie jednostki (jak moc pisania)
Metoda 2 z 7: trapez
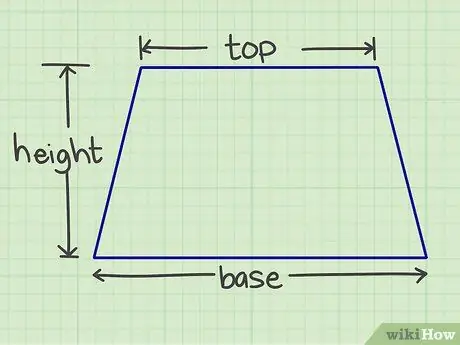
Krok 1. Zmierz wymaganą liczbę
Musisz zmierzyć podstawę, dach i wysokość. Podstawa i dach są równoległymi bokami, a wysokość jest prostopadłą linią łączącą dwa równoległe boki.
W prawdziwym świecie może być konieczne samodzielne zmierzenie, ale jeśli chodzi o odrabianie lekcji, nauczyciel zwykle zapisał już liczby wraz ze zdjęciem kształtu
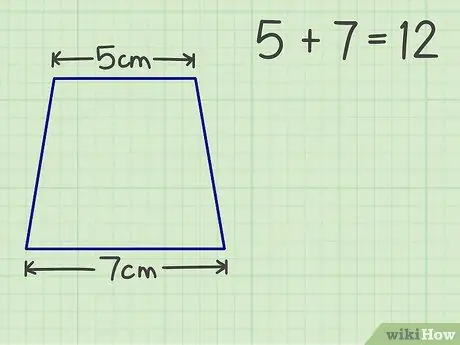
Krok 2. Dodaj dwie równoległe strony
Na przykład nasz trapez ma dach 5 cm i podstawę 7 cm. Suma dwóch równoległych boków wynosi 12.
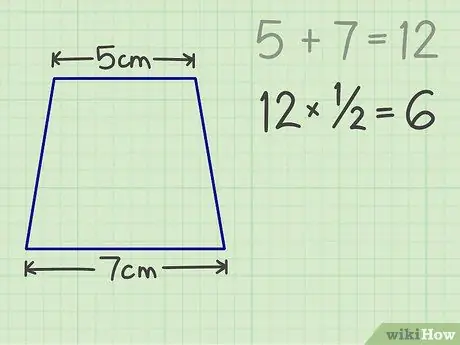
Krok 3. Pomnóż liczbę przez 1/2, wynik to 6
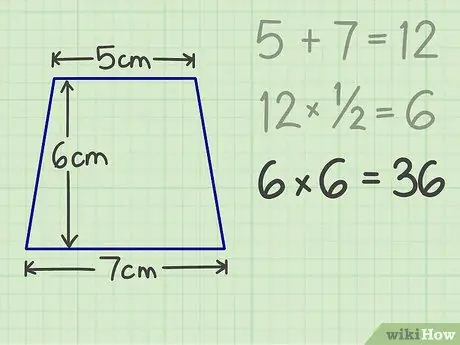
Krok 4. Następnie pomnóż wynik przez wysokość
Na przykład, jeśli trapez ma wysokość 6 cm, końcowy wynik to 36.
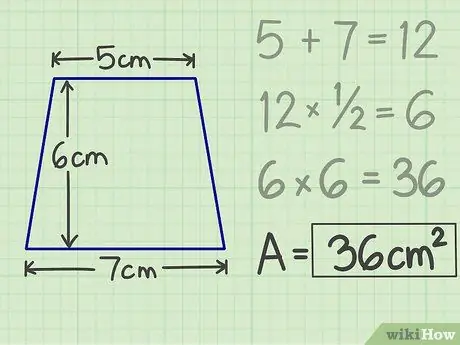
Krok 5. Zapisz wyniki
Mnożenie, które wykonałeś wcześniej, da liczbę, a mianowicie obszar trapezu. Czyli dla trapezu z dachem 5 cm, podstawą 7 cm i wysokością 6 cm powierzchnia to 36 cm kwadratu.
Metoda 3 z 7: Koło
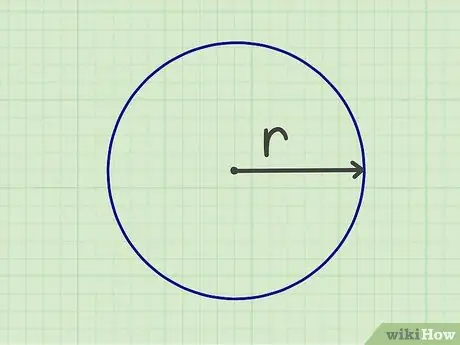
Krok 1. Zmierz promień
Aby móc obliczyć powierzchnię koła, musisz zmierzyć promień. promień to odległość od środka okręgu do jego krawędzi. Możesz również zmierzyć promień, mierząc średnicę (szerokość okręgu od krawędzi do krawędzi), a następnie dzieląc liczbę przez dwa.
W prawdziwym świecie może być konieczne samodzielne zmierzenie, ale jeśli chodzi o odrabianie lekcji, nauczyciel zwykle zapisał już liczby wraz ze zdjęciem kształtu
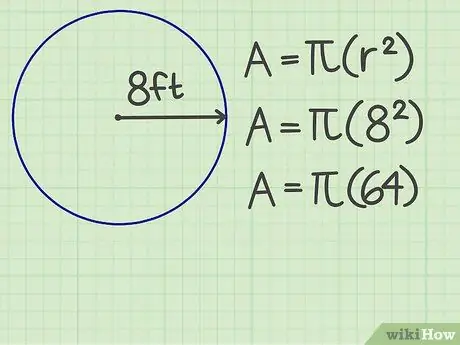
Krok 2. Wyprostuj palce
Pomnóż przez samą liczbę promieni. Na przykład promień okręgu wynosi 8 stóp, więc wynik to 64.
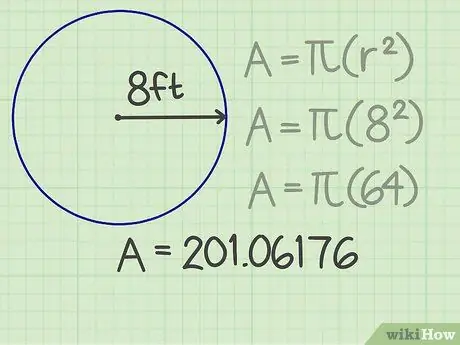
Krok 3. Pomnóż wynik przez pi
Pi (π) to ważna liczba używana w różnych formułach. Jeśli używasz kalkulatora, naciśnij klawisz pi, aby uzyskać naprawdę dokładne wyniki. W przeciwnym razie, aby ułatwić sobie obliczenia, możesz zaokrąglić pi do kilku cyfr po przecinku, na przykład 3, 14159. Po pomnożeniu tej liczby przez kwadrat promienia otrzymamy wynik 201, 06176.
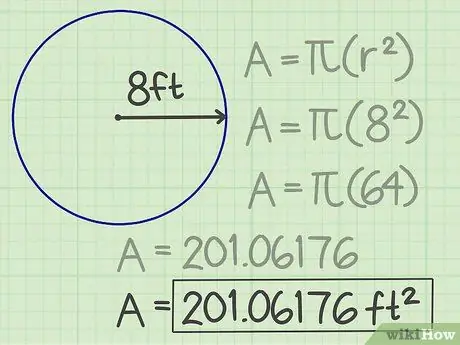
Krok 4. Zapisz wyniki
Otrzymana liczba, 201, 06176 to powierzchnia koła. Tak więc jego powierzchnia wynosi 201,06176 stóp kwadratowych.
Metoda 4 z 7: Sektor (Juring)
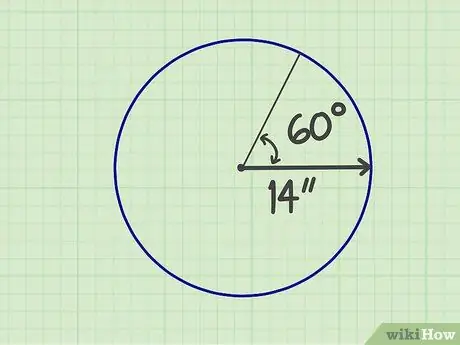
Krok 1. Zmierz wymagane liczby
Sektor to wycinek koła utworzony przez dwa promienie i krawędź, dzięki czemu kształt przypomina wachlarz. Musisz znać rozmiar promienia i kąt, z którego składa się „wentylator”. Załóżmy na przykład, że sektor ma promień 14 cali i kąt 60 stopni.
W prawdziwym świecie może być konieczne samodzielne zmierzenie, ale jeśli chodzi o odrabianie lekcji, nauczyciel zwykle zapisał już liczby wraz ze zdjęciem kształtu
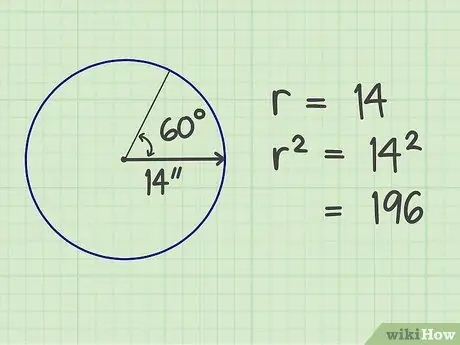
Krok 2. Wyprostuj palce
Pomnóż przez samą liczbę promieni. Wynik to 196 (14x14).

Krok 3. Pomnóż wynik przez pi
Pi (π) to ważna liczba używana w różnych formułach. Jeśli używasz kalkulatora, naciśnij klawisz pi, aby uzyskać naprawdę dokładne wyniki. W przeciwnym razie, aby ułatwić sobie obliczenia, możesz zaokrąglić pi do kilku cyfr po przecinku, na przykład 3, 14159. Jeśli pomnożysz tę liczbę przez kwadrat promienia, otrzymamy 615, 75164.

Krok 4. Podziel miarę kąta przez 360
Podziel kąt wentylatora sektorowego przez 360 (miara kąta pełnego koła). W powyższym przykładzie wynik wynosi około 0,166. Jeśli obliczysz go za pomocą kalkulatora, wynik jest w rzeczywistości dłuższy i iteracyjny, ale tutaj jest zaokrąglony, aby ułatwić obliczenia.

Krok 5. Pomnóż tę liczbę przez poprzednią liczbę
Pomnóż liczbę otrzymaną po podzieleniu kąta przez 360 przez liczbę otrzymaną wcześniej po pomnożeniu pi przez kwadrat promienia. w powyższym przykładzie wynik to 102, 214 (po zaokrągleniu).
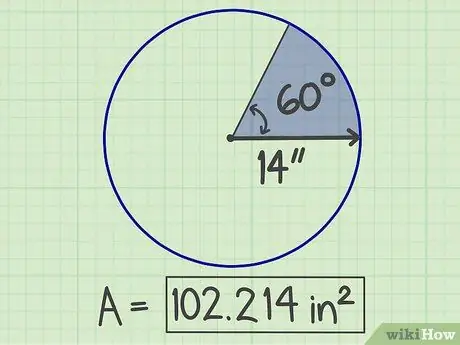
Krok 6. Zapisz wyniki
Otrzymana liczba to powierzchnia sektora, która wynosi 102 214 cali kwadratowych.
Metoda 5 z 7: Elipsa
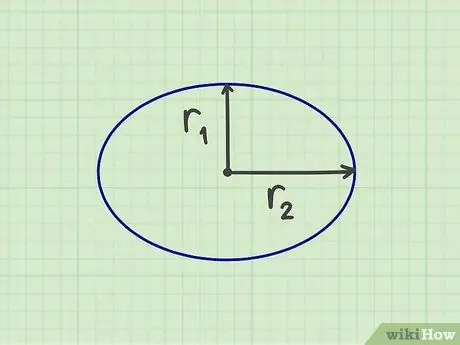
Krok 1. Zmierz wymaganą liczbę
Aby obliczyć powierzchnię elipsy, należy zmierzyć dwa „promienie”, a mianowicie promień krótki i promień długi, który stanowi połowę szerokości i połowę wysokości elipsy. Można również zmierzyć krótki promień od środka elipsy do najkrótszego boku oraz długi promień od środka elipsy do najdłuższego boku. Krótki promień powinien tworzyć kąt prosty do długiego promienia.
W prawdziwym świecie może być konieczne samodzielne zmierzenie, ale jeśli chodzi o odrabianie lekcji, nauczyciel zwykle zapisał już liczby wraz ze zdjęciem kształtu
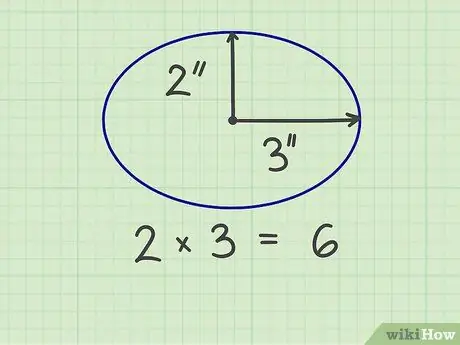
Krok 2. Pomnóż dwa palce
Na przykład elipsa ma 6 cali szerokości i 4 cale wysokości, więc promienie mają 3 cale i 2 cale. Po pomnożeniu tych dwóch liczb wynik wynosi 6 (3 x 2).

Krok 3. Pomnóż wynik przez pi
Pi (π) to ważna liczba używana w różnych formułach. Jeśli używasz kalkulatora, naciśnij klawisz pi, aby uzyskać naprawdę dokładne wyniki. W przeciwnym razie, aby ułatwić sobie obliczenia, możesz zaokrąglić pi do kilku cyfr po przecinku, na przykład 3, 14159. Po pomnożeniu tej liczby przez kwadrat promienia otrzymamy 18, 84954.
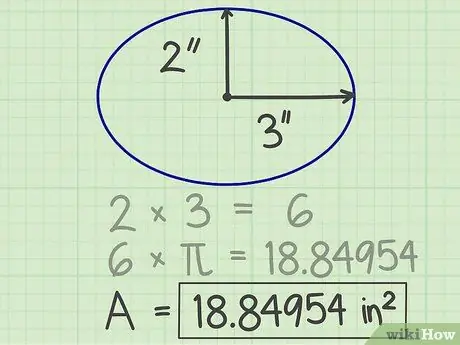
Krok 4. Zapisz wyniki
Liczba uzyskana z powyższego obliczenia to obszar elipsy. W powyższym przykładzie powierzchnia elipsy wynosi 18,84954 cali kwadratowych.
Metoda 6 z 7: Trójkąt
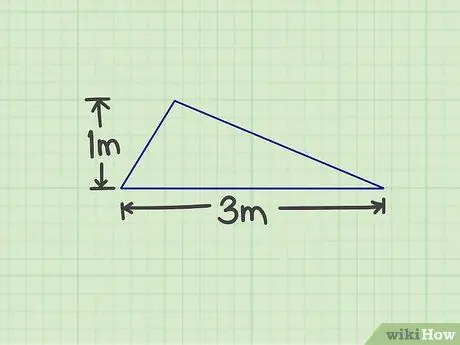
Krok 1. Zmierz wymaganą liczbę
Musisz zmierzyć podstawę i wysokość trójkąta. Podstawą może być dowolny bok trójkąta, o ile możesz zmierzyć wysokość. Na przykład jest trójkąt o podstawie 3 mi wysokości 1 m.
W prawdziwym świecie może być konieczne samodzielne zmierzenie, ale jeśli chodzi o odrabianie lekcji, nauczyciel zwykle zapisał już liczby wraz ze zdjęciem kształtu
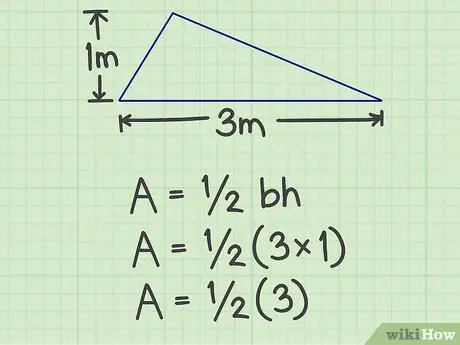
Krok 2. Pomnóż podstawę przez wysokość
W powyższym przykładzie wynik to 3 (3x1).
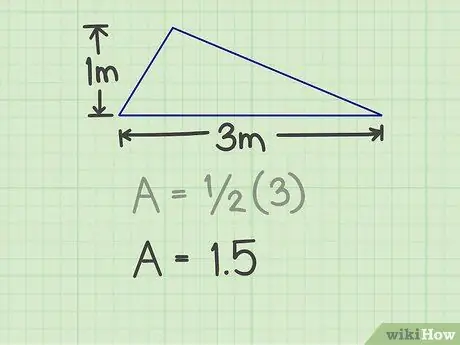
Krok 3. Pomnóż wynik przez 1/2
To mnożenie da liczby 1, 5.
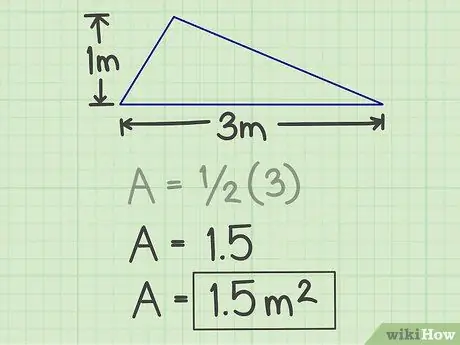
Krok 4. Zapisz wyniki
Liczba wygenerowana przez powyższe obliczenie to obszar trójkąta, a w powyższym przykładzie jego powierzchnia wynosi 1,5 metra kwadratowego.
Metoda 7 z 7: Złożona konstrukcja płaska
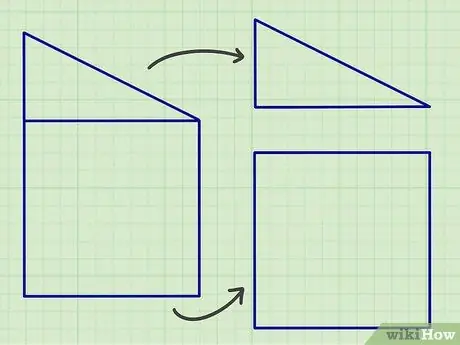
Krok 1. Oddziel złożone kształty płaszczyzn na części składające się ze standardowych kształtów geometrycznych powyżej
Jeśli to, co robisz, to praca domowa, może być łatwo podzielić złożony kształt na płaskie kształty omówione wcześniej, ale w prawdziwym świecie może być konieczne podzielenie płaskiego kształtu na wiele płaskich kształtów, aby uzyskać dokładny wynik obliczeń.
Dobrym sposobem na rozpoczęcie jest szukanie linii równoległych lub tworzących pewien kąt, ponieważ większość płaskich kształtów składa się z tych kształtów
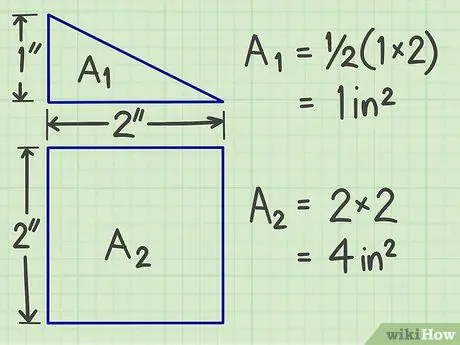
Krok 2. Oblicz pole dla każdej z figur płaskich wynikające z separacji
Użyj powyższych metod, aby uzyskać obszar każdego płaskiego kształtu.
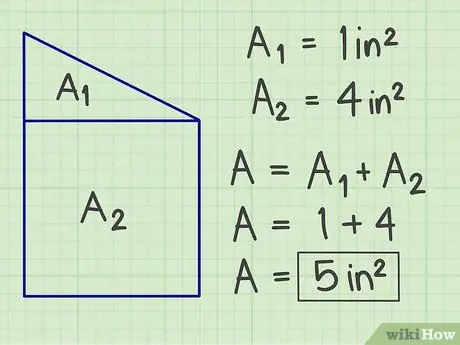
Krok 3. Zsumuj wyniki
Dodaj wszystkie obliczone obszary, aby uzyskać całkowity obszar złożonej figury samolotu.
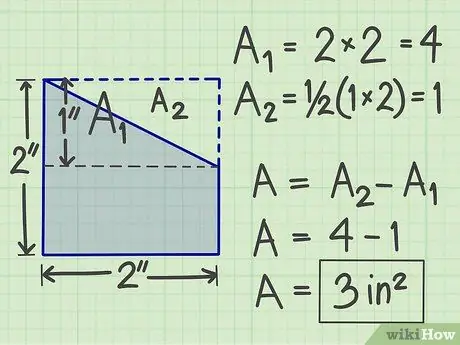
Krok 4. Użyj innej metody
Istnieje wiele innych sposobów, które możesz wypróbować, w zależności od kształtu złożonego płaskiego kształtu. Na przykład można również dodać do niego wyimaginowany kształt płaszczyzny, aby stał się standardowym geometrycznym kształtem płaszczyzny. Następnie oblicz obszar, a następnie odejmij obszar wyimaginowanego płaskiego kształtu, którego użyłeś do dodania.
Porady
- Użyj tego kalkulatora, jeśli potrzebujesz pomocy w rozwiązywaniu obliczeń matematycznych.
- Poproś znajomego o pomoc, jeśli nadal masz problemy!
Ostrzeżenie
- Zawsze lepiej sprawdzić wyniki obliczeń, aby upewnić się, że są poprawne!
- Upewnij się, że wszystkie jednostki, których używasz, są takie same (cm, m, cale itp.) podczas obliczania, aby nie pomylić się z powodu mieszanych jednostek!






