- Autor Jason Gerald [email protected].
- Public 2024-01-16 19:50.
- Ostatnio zmodyfikowany 2025-06-01 06:07.
Szybkość to obliczenie, jak szybko coś się porusza w danym momencie. Jeśli kiedykolwiek spojrzałeś na prędkościomierz jadącego samochodu, zobaczysz licznik prędkości - im dalej porusza się wskazówka, tym większa prędkość pojazdu. Istnieje kilka sposobów obliczania prędkości, w zależności od rodzaju posiadanych informacji. Ogólnie formuła prędkość = odległość/czas (lub k = j/w) to najprostszy sposób obliczenia prędkości.
Krok
Metoda 1 z 3: Korzystanie ze standardowych formuł obliczania prędkości

Krok 1. Znajdź odległość, jaką przebył obiekt
Podstawowa formuła, której większość ludzi używa, aby znaleźć prędkość czegoś, jest bardzo łatwa w użyciu. Przede wszystkim trzeba wiedzieć „jak dużą odległość przebył mierzony obiekt”. Innymi słowy, jaka jest odległość między punktem początkowym a końcowym obiektu?
Ta formuła jest łatwiejsza do zrozumienia na przykładzie. Powiedzmy, że jedziemy autem na plac zabaw przez „161 kilometrów”. W kilku krokach możemy wykorzystać te informacje do zakończenia obliczania wzoru

Krok 2. Znajdź czas potrzebny obiektowi na pokonanie tej odległości
Następną potrzebną informacją jest to, ile czasu zajmuje obiektowi dotarcie do określonej odległości. Innymi słowy, ile czasu zajmuje przesunięcie obiektu z punktu początkowego do punktu końcowego?
W tym przykładzie załóżmy, że obiekt zajmuje ok. dwie godziny dotrzeć do celu.

Krok 3. Podziel odległość przez czas potrzebny na znalezienie prędkości obiektu
Potrzebujesz tylko tych dwóch informacji, aby poznać prędkość obiektu. Odległość do czasu jest równa prędkości obiektu.
W tym przykładzie 161 kilometrów/2 godziny = 80,5 kilometrów na godzinę.

Krok 4. Nie zapomnij o używanym urządzeniu
Bardzo ważne jest, aby w odpowiedzi używać poprawnych jednostek (takich jak kilometry na godzinę itp.) Bez tych jednostek ludziom bardzo trudno jest zrozumieć znaczenie twojej odpowiedzi. Możesz również stracić punkty, jeśli użyjesz niewłaściwej jednostki podczas wykonywania zadań ze szkoły.
Jednostką prędkości jest jednostka odległości do jednostki czasu. Na przykład, ponieważ mierzymy odległość w kilometrach, a czas w godzinach, używane jednostki to kilometry/godzinę (lub kilometrów na godzinę).
Metoda 2 z 3: Rozwiązywanie trudniejszych obliczeń

Krok 1. Znajdź kilka różnych zmiennych, aby rozwiązać problem odległości i czasu
Po zrozumieniu podstawowego wzoru na szybkość możesz go używać do wykonywania obliczeń innych niż szybkość. Na przykład, jeśli na początku znasz tylko prędkość obiektu i jedną inną zmienną, możesz zmienić powyższy wzór, aby znaleźć nieznaną informację.
-
Załóżmy na przykład, że wiemy, że pociąg jedzie z prędkością 20 kilometrów na godzinę przez cztery godziny, ale nie wiemy, jak daleko przebył. Aby się tego dowiedzieć, możemy przearanżować formułę w następujący sposób:
-
- prędkość = odległość/czas
- prędkość × czas = (odległość/czas) × czas
- prędkość × czas = odległość
- 20 km/h × 4 godziny = odległość = 80 kilometrów
-

Krok 2. W razie potrzeby przekonwertuj używane jednostki
Czasami możesz obliczyć prędkość za pomocą określonej jednostki, ale musisz przeliczyć ją na inną jednostkę. W takim przypadku musisz użyć współczynnika konwersji, aby uzyskać odpowiedź zgodnie z poprawnymi jednostkami. Aby to zrobić, po prostu napisz relację między jednostkami w postaci ułamka i pomnóż. Podczas mnożenia odwróć ułamek w razie potrzeby, aby usunąć niechciane jednostki. Ta metoda jest znacznie łatwiejsza niż się wydaje!
-
Załóżmy na przykład, że w powyższym przykładzie potrzebujemy odpowiedzi w milach zamiast w kilometrach. Jedna mila to około 1,6 kilometra. Tak więc możemy dokonać konwersji w następujący sposób:
-
- 80 kilometrów × 1 mila/1,6 kilometra = 50 mil
-
- Pamiętaj, ponieważ kilometry pojawiają się na dole ułamka, usuwa kilometry z poprzedniej odpowiedzi, więc końcowy wynik wykorzystuje mile.
- Ta strona internetowa zapewnia funkcje konwersji dla większości powszechnie używanych jednostek.

Krok 3. W razie potrzeby zastąp zmienną „odległość” formułą odległości
Obiekty nie zawsze poruszają się po prostej, gładkiej ścieżce. Jeśli to prawda, możesz nie być w stanie po prostu wpisać wartości liczbowej jako jednostki odległości do standardowego wzoru na prędkość. Jednak może być konieczne zastąpienie litery j we wzorze k = j/w formułą przypominającą odległość przebytą przez obiekt.
-
Załóżmy na przykład, że samolot obraca się w powietrzu na odległość 20 mil 5 razy. Samolot ukończył rundę w pół godziny. W tym przykładzie nadal musimy znaleźć całkowitą odległość przebytą przez samolot, zanim będziemy mogli określić jego prędkość. Możemy użyć wzoru do obliczania odległości wokół okręgu (odległość wokół niego) zamiast j w tym wzorze. Wzór ten to obwód = 2πr gdzie r = promień okręgu. Oto jak to rozwiązać:
-
- k = (2 × × r)/w
- k = (2 × × 10)/0,5
- k = 62,83/0,5 = 125,66 mil na godzinę
-

Krok 4. Zrozum, że k = j/w daje średnią prędkość
Łatwy i prosty wzór, którego używamy do obliczania prędkości, ma jedną wadę. Wynikowa wartość jest technicznie średnią prędkością. Oznacza to, że wzór zakłada, że mierzony obiekt porusza się z taką samą prędkością. Jak zobaczymy poniżej, znalezienie prędkości obiektu w jednej chwili będzie znacznie trudniejsze.
Aby zilustrować tę różnicę, wyobraź sobie, kiedy ostatnio podróżowałeś samochodem. Jest mało prawdopodobne, że będziesz podróżować z taką samą prędkością, jak podróżujesz. Jednak zazwyczaj rozpoczynasz podróż z małą prędkością i stopniowo zwiększasz prędkość po drodze, zatrzymując się z powodu czerwonych świateł, korków itp. Jeśli używasz standardowego wzoru na prędkość, aby znaleźć prędkość podczas jazdy, zmiany tej prędkości nie zostaną wykryte. Otrzymasz jednak odpowiedź, która pokazuje średnią prędkość wszystkich różnic prędkości, które podróżujesz
Metoda 3 z 3: Obliczanie prędkości natychmiastowej
Notatka:
Ta sekcja wykorzystuje techniki, które są mniej znane osobom, które nigdy nie studiowały rachunku różniczkowego. Przeczytaj nasze artykuły na temat rachunku różniczkowego, aby uzyskać pomoc.
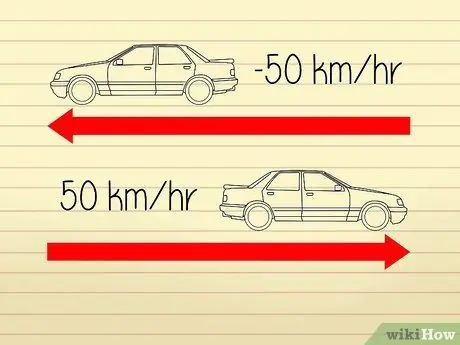
Krok 1. Zrozum, że prędkość jest definiowana jako tempo przyspieszenia
Obliczenia prędkości na wysokim poziomie są dość mylące, ponieważ matematycy i naukowcy używają różnych definicji do opisania „prędkości” i „przyspieszenia”. Przyspieszenie składa się z dwóch elementów: „szybkości” i „kierunku”. Szybkość jest równa prędkości obiektu. Zmiana kierunku spowoduje zmianę przyspieszenia, ale nie zmianę prędkości.
- Załóżmy na przykład, że dwa samochody poruszają się w przeciwnych kierunkach. Prędkościomierze w obu samochodach wyświetlają wartość 50 km/h, więc oba poruszają się z tą samą prędkością. Ponieważ jednak samochody oddalają się od siebie, możemy powiedzieć, że jeden z samochodów ma „przyspieszenie” -50 km/h, podczas gdy drugi ma „przyspieszenie” 50 km/h.
- Podobnie jak obliczenia prędkości chwilowej, można również wykonać obliczenia przyspieszenia chwilowego.

Krok 2. Użyj wartości bezwzględnych do pomiaru przyspieszenia ujemnego
Obiekt może mieć ujemne tempo przyspieszenia (jeśli porusza się w kierunku ujemnym względem innego obiektu). Nie ma jednak prędkości ujemnej. Tak więc w tym przypadku wartość bezwzględna szybkości wskazuje prędkość obiektu.
Z tego powodu w przykładzie powyżej oba samochody mają prędkość 50km/h.
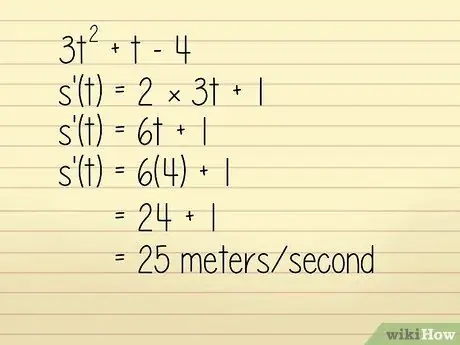
Krok 3. Weź pochodną pozycji funkcji
Jeśli masz funkcję k(w), która pokazuje położenie obiektu bez konieczności obliczania czasu, pochodna k(w) pokaże przyspieszenie bez potrzeby mierzenia czasu. Po prostu wstaw wartość czasu do tego wzoru, aby zmienna w (lub jakakolwiek użyta wartość czasu) została przyspieszona zgodnie z tym czasem. Stąd możesz łatwo znaleźć prędkość obiektu.
-
Załóżmy na przykład, że położenie obiektu w metrach opisuje równanie 3q2 + w - 4 gdzie w = czas w sekundach. Chcemy poznać prędkość obiektu w = 4 sekundy. W takim przypadku możesz to rozwiązać poprzez:
-
- 3w2 +w - 4
- k'(w) = 2 × 3w + 1
- k'(w) = 6w + 1
-
-
Teraz wpisujemy w = 4:
-
- k'(w) = 6(4) + 1 = 24 + 1 = 25 metrów/sekundę. Technicznie jest to obliczenie przyspieszenia, ale ponieważ jest ono dodatnie, a kierunek nie jest wymieniony w pytaniu, możemy go użyć do obliczenia prędkości.
-

Krok 4. Weź funkcję przyspieszenia całkowego
Przyspieszenie to sposób pomiaru zmiany przyspieszenia obiektu w czasie. Ten temat jest zbyt złożony, aby można go było w pełni wyjaśnić w tym artykule. Jednak warto zauważyć, że gdy masz funkcję a(w), która reprezentuje przyspieszenie w czasie, całka a(w) zwróci wynik przyspieszenia oparty na tym czasie. Pamiętaj, że bardzo przydatne jest poznanie początkowego przyspieszenia obiektu, aby móc zdefiniować stałą tego wyniku z nieskończonej całki.
-
Na przykład załóżmy, że obiekt ma stałe przyspieszenie (wm/s2 w wyniku a(w) = -30. Powiedz również, że obiekt ma początkowe przyspieszenie 10 m/s. Musimy znaleźć prędkość w w = 12 sekund. W takim przypadku możemy to rozwiązać poprzez:
-
- a(w) = -30
- p(w)= a(w)dw = -30dw = -30w + C
-
-
Aby znaleźć C, rozwiążemy p(w) dla w = 0. Pamiętaj, że początkowe przyspieszenie obiektu wynosi 10 m/s.
-
- p(0) = 10 = -30(0) + C
- 10 = C, więc p(w) = -30w + 10
-
-
Teraz możemy wpisać w = 12 sekund.
-
- p(12) = -30(12) + 10 = -360 + 10 = -350. Ponieważ prędkość jest wartością bezwzględną przyspieszenia, prędkość obiektu wynosi 350 metrów/sekundę.
-
Porady
- Praktyka czyni mistrza! Spróbuj stworzyć własne pytanie, zastępując liczby w powyższym przykładzie.
- Jeśli szukasz szybkiego sposobu na ćwiczenie rachunku różniczkowego w celu uzyskania większej szybkości obliczeń, skorzystaj z internetowego kalkulatora pochodnego tutaj i internetowego kalkulatora całkowego tutaj.






