Odwrotność lub odwrotność jest bardzo przydatna we wszelkiego rodzaju równaniach algebraicznych. Na przykład, kiedy dzielisz jeden ułamek przez drugi, mnożysz pierwszy ułamek przez odwrotność drugiego. Musisz również użyć odwrotności, gdy szukasz równania prostej.
Krok
Metoda 1 z 3: Znajdowanie odwrotności ułamka lub liczby całkowitej
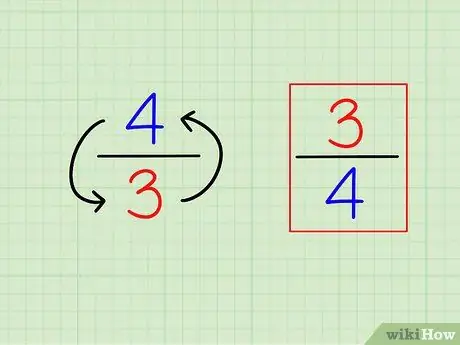
Krok 1. Znajdź odwrotność ułamka, odwracając go
Definicja „wzajemności” lub przeciwnie jest bardzo prosta. Aby znaleźć odwrotność dowolnej liczby całkowitej, po prostu oblicz „1 (ta liczba)”. W przypadku ułamków odwrotność to inny ułamek, to znaczy liczby są „odwrócone” (odwrotność).
- Na przykład przeciwieństwo 3/4 jest 4/3.
- Dowolna liczba pomnożona przez jej odwrotność zwraca 1.
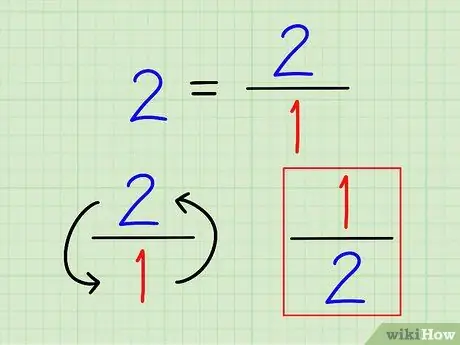
Krok 2. Zapisz odwrotność liczby całkowitej jako ułamek
Odwrotność liczby to zawsze 1 (ta liczba). W przypadku liczb całkowitych zapisz je jako ułamki. Nie ma sensu obliczać tej liczby z ułamkiem dziesiętnym.
Na przykład odwrotność 2 to 1 2 = 1/2.
Metoda 2 z 3: Znajdowanie odwrotności ułamka mieszanego
Krok 1. Zidentyfikuj liczby mieszane
Ułamki mieszane składają się z liczb całkowitych i ułamków, takich jak 24/5. Istnieją dwa kroki, aby znaleźć odwrotność liczby mieszanej, jak opisano poniżej.
Krok 2. Zamiana liczb mieszanych na ułamki niewłaściwe
Pamiętaj, że 1 zawsze można zapisać jako (liczba)/(ta sama liczba), a ułamki o tym samym mianowniku (liczba dolna) można dodawać razem. Oto przykład z użyciem 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
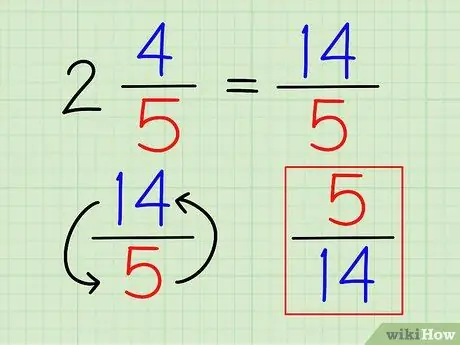
Krok 3. Odwróć ułamek
Gdy liczba zostanie zapisana w całości jako ułamek, możesz znaleźć jej odwrotność, tak jak każdy inny ułamek, odwracając ułamek.
W powyższym przykładzie odwrotność 14/5 jest 5/14.
Metoda 3 z 3: Znajdowanie przeciwieństwa liczby dziesiętnej
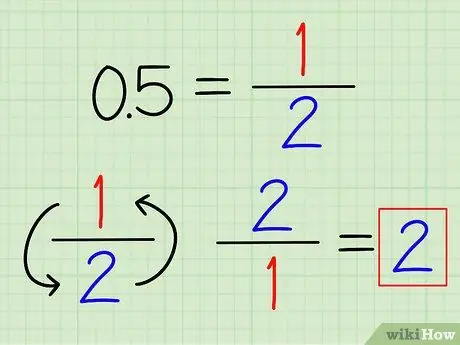
Krok 1. Jeśli to możliwe, przekształć ułamki dziesiętne na ułamki zwykłe
Możesz rozpoznać niektóre często używane liczby dziesiętne, które można łatwo przekonwertować na ułamki. Na przykład 0,5 = 1/2 i 0,25 = 1/4. Po przeliczeniu ułamka dziesiętnego na ułamek po prostu odwróć ułamek, aby znaleźć jego odwrotność.
Na przykład odwrotność 0,5 to 2/1 = 2.
Krok 2. Napisz zadanie dzielenia
Jeśli nie możesz przeliczyć tego na ułamek, oblicz odwrotność liczby w postaci zadania dzielenia: 1 (dziesiętny). Możesz użyć kalkulatora, aby go rozwiązać lub przejść do następnego kroku, aby rozwiązać go ręcznie.
Na przykład możesz znaleźć odwrotność 0,4, obliczając 1 0,4
Krok 3. Zmień problem dzielenia na liczby całkowite
Pierwszym krokiem do dzielenia miejsc dziesiętnych jest przesunięcie punktu dziesiętnego, aż wszystkie liczby będą liczbami całkowitymi. Dopóki przesuniesz przecinek dziesiętny obu liczb o tę samą liczbę kroków, otrzymasz prawidłową odpowiedź.
Na przykład możesz użyć 1 0, 4 i przepisać je jako 10 4. W tym przypadku wszystkie miejsca dziesiętne przesuwasz o jeden krok w prawo, w ten sam sposób, w jaki mnożysz każdą liczbę przez dziesięć
Krok 4. Rozwiąż problem, używając dzielenia długiego
Użyj metody dzielenia długiego, aby obliczyć odwrotność. Jeśli policzysz 10 4, otrzymasz odpowiedź 2, 5 co jest odwrotnością 0, 4.
Porady
- Odwrotność ujemna liczby jest taka sama jak odwrotność regularna, ponieważ jest mnożona przez ujemną. Na przykład ujemna odwrotność 3/4 jest -4/3.
- Odwrotność lub odwrotność jest często określana jako „odwrotność mnożenia”.
- Liczba 1 jest jej przeciwieństwem, ponieważ 1 1 = 1.
- Liczba 0 nie ma odwrotności, ponieważ 0 jest niezdefiniowane.
