Dodawanie ułamków to bardzo przydatna wiedza. Ta umiejętność jest bardzo łatwa do nauczenia i wykorzystania podczas pracy nad zadaniami matematycznymi od podstawówki do liceum. W tym artykule wyjaśniono, jak dodawać ułamki, aby zrobić to w kilka minut.
Krok
Metoda 1 z 2: Dodawanie ułamków o tym samym mianowniku
Krok 1. Sprawdź mianownik (liczbę pod ilorazem) każdej frakcji
Jeśli liczby są takie same, dodajesz ułamki o tym samym mianowniku. Jeśli mianowniki są różne, przeczytaj drugą metodę.
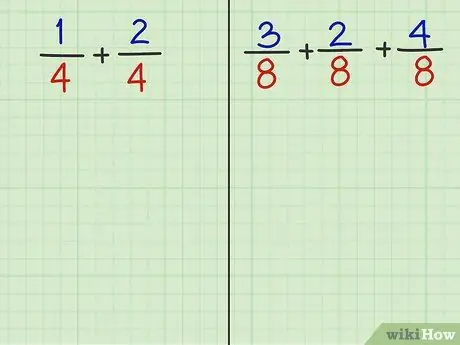
Krok 2. Odpowiedz na 2 pytania
Czytając ostatni krok w tej metodzie, powinieneś być w stanie zsumować ułamki z następujących dwóch pytań.
- Problem 1: 1/4 + 2/4
- Problem 2: 3/8 + 2/8 + 4/8
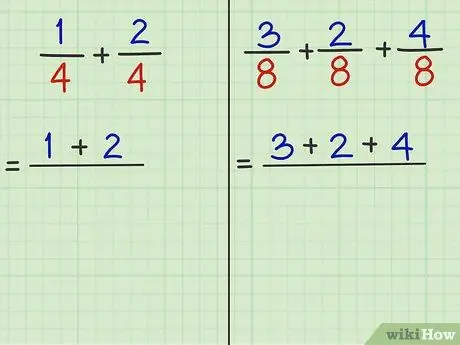
Krok 3. Zbierz liczniki (liczby powyżej podziału) i dodaj je
Licznik to liczba powyżej ilorazu. Bez względu na to, ile ułamków chcesz dodać, możesz dodać liczniki od razu, jeśli mianowniki są takie same.
- Problem 1: 1/4 + 2/4 to ułamek do dodania. „1” i „2” to liczniki. Tak więc 1 + 2 = 3.
- Problem 2: 3/8 + 2/8 + 4/8 to ułamek do dodania. „3” i „2” i „4” są licznikami. Tak więc 3 + 2 + 4 = 9.
Krok 4. Określ nowy ułamek z sumy
Zapisz licznik uzyskany w kroku 2. Ta liczba to nowy licznik. Wpisz mianownik, który jest taką samą liczbą pod dwusieczną każdego ułamka. Nie musisz wykonywać obliczeń, jeśli mianowniki są takie same. Ta liczba to nowy mianownik i zawsze równa się staremu mianownikowi, gdy dodajesz ułamki o tym samym mianowniku.
- Problem 1: 3 to nowy licznik, a 4 to nowy mianownik. Zatem odpowiedź na pytanie 1 to 3/4. 1/4 + 2/4 = 3/4.
- Problem 2: 9 to nowy licznik, a 8 to nowy mianownik. Zatem odpowiedź na pytanie 2 to 9/8. 3/8 + 2/8 + 4/8 = 9/8.
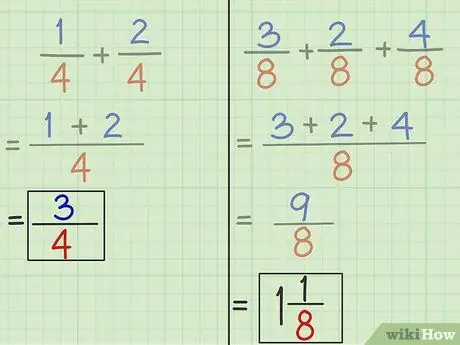
Krok 5. W razie potrzeby uproszcz ułamki
Nie zapomnij uprościć nowego ułamka, aby ułatwić pisanie.
-
Jeśli licznik większy zamiast mianownika, takiego jak wynik dodawania problemu 2, oznacza to, że po uproszczeniu ułamka otrzymujemy 1 cały miesiąc. Podziel licznik przez mianownik lub 9 podzielone przez 8. Wynik jest liczbą całkowitą 1 pozostała 1. Napisz liczby całkowite przed ułamkiem, a reszta staje się licznikiem nowego ułamka o tym samym mianowniku.
9/8 = 1 1/8.
Metoda 2 z 2: Dodawanie ułamków o różnych mianownikach
Krok 1. Sprawdź mianownik (liczbę pod ilorazem) każdej frakcji
Jeśli mianowniki są różne, jesteś dodaj ułamki o różnych mianownikach. Przeczytaj poniższe kroki, ponieważ przed dodaniem ułamków musisz wyrównać mianowniki.
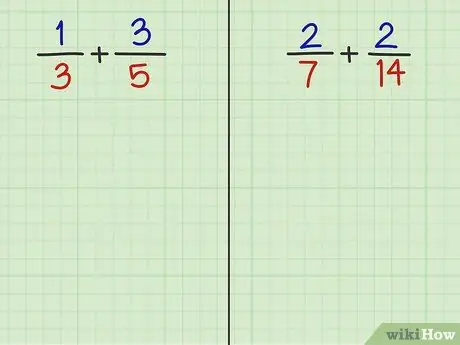
Krok 2. Rozwiąż następujące 2 pytania
Czytając ostatni krok w tej metodzie, powinieneś być w stanie zsumować ułamki z następujących dwóch pytań.
- Problem 3: 1/3 + 3/5
- Pytanie 4: 2/7 + 2/14
Krok 3. Dopasuj mianowniki
Aby to zrobić, pomnóż mianowniki dwóch powyższych ułamków. Prostym sposobem na wyrównanie mianowników jest pomnożenie mianowników dwóch ułamków. Jeśli jeden z mianowników jest wielokrotnością drugiego, znajdź najmniejszą wspólną wielokrotność dwóch mianowników.
-
Problem 3:
3 x 5 = 15. Tak więc nowy mianownik obu ułamków to 15.
-
Problem 4:
14 jest wielokrotnością 7. Dlatego wystarczy pomnożyć 7 przez 2, aby otrzymać 14. Zatem nowy mianownik obu ułamków to 14.
Krok 4. Pomnóż licznik i mianownik pierwszego ułamka przez mianownik drugiego ułamka
Ten krok nie zmienia wartości ułamka, ale ułamek wygląda na zmianę, aby pasował do mianownika. Wartość ułamkowa pozostaje taka sama.
-
Problem 3:
1/3 x 5/5 = 5/15.
-
Problem 4:
W przypadku tego problemu wystarczy pomnożyć pierwszy ułamek przez 2/2, aby uzyskać równe mianowniki.
2/7 x 2/2 = 4/14
Krok 5. Pomnóż licznik i mianownik drugiego ułamka przez mianownik pierwszego ułamka
Podobnie jak w powyższych krokach, nie zmieniamy wartości ułamka, ale ułamek wygląda na zmianę, aby wyrównać mianownik. Wartość ułamkowa pozostaje taka sama.
-
Problem 3:
3/5 x 3/3 = 9/15.
-
Problem 4:
Nie musimy mnożyć drugiego ułamka, ponieważ mianowniki są takie same.
Krok 6. Zapisz kolejno dwie nowe frakcje
W tym momencie nie dodaliśmy dwóch ułamków razem, chociaż możemy. W powyższym kroku pomnożyliśmy każdy ułamek przez 1. Teraz chcemy się upewnić, że ułamki, które chcemy dodać, mają ten sam mianownik.
-
Problem 3:
zamiast 1/3 + 3/5 ułamek staje się 5/15 + 9/15
-
Problem 4:
Zamiast 2/7 + 2/14 ułamek staje się 4/14 + 2/14
Krok 7. Dodaj liczniki dwóch ułamków razem
Licznik to liczba powyżej ilorazu.
-
Problem 3:
5 + 9 = 14. 14 to nowy licznik.
-
Problem 4:
4 + 2 = 6. 6 to nowy licznik.
Krok 8. Wpisz wspólny mianownik (w kroku 2) pod nowym licznikiem lub użyj mianownika ułamka pomnożonego przez 1, aby wyrównać mianownik
-
Problem 3:
15 to nowy mianownik.
-
Problem 4:
14 to nowy mianownik.
Krok 9. Napisz nowy licznik i nowy mianownik
-
Problem 3:
14/15 to odpowiedź 1/3 + 3/5 = ?
-
Problem 4:
6/14 to odpowiedź 2/7 + 2/14 = ?
Krok 10. Uprość i zmniejsz ułamki
Aby uprościć ułamki, podziel licznik i mianownik przez największy wspólny dzielnik tych dwóch liczb.
-
Problem 3:
14/15 nie można uprościć.
-
Problem 4:
6/14 można zmniejszyć do 3/7 po podzieleniu licznika i mianownika przez 2 jako największy wspólny dzielnik 6 i 14.
Porady
- Przed dodaniem ułamków upewnij się, że mianowniki są takie same.
- Nie sumuj mianowników. Jeśli mianowniki są takie same, użyj liczby jako mianownika po dodaniu ułamków.
- Jeśli chcesz dodać ułamki z liczbami składającymi się z liczb całkowitych i ułamków, przekonwertuj te liczby na ułamki i dodaj je zgodnie z powyższymi instrukcjami.
