W statystyce zakres to różnica między najwyższą wartością w zestawie danych a najniższą wartością w zestawie danych. Zakres pokazuje, jak rozłożone są wartości w szeregu. Jeśli zakres jest dużą liczbą, wartości w serii są bardzo rozproszone; jeśli zakres jest małą liczbą, to wartości w serii są do siebie zbliżone. Jeśli chcesz wiedzieć, jak obliczyć zasięg, wykonaj następujące kroki.
Krok
Krok 1. Wymień elementy swojego zbioru danych
Aby znaleźć zakres zestawu danych, musisz wymienić wszystkie elementy w zestawie danych, aby móc zidentyfikować największe i najmniejsze liczby. Zapisz wszystkie elementy. Liczby w tym zestawie danych to: 14, 19, 20, 24, 25 i 28.
- Łatwiej jest zidentyfikować największe i najmniejsze liczby w zestawie danych, jeśli uporządkujesz liczby od najmniejszej do największej. W tym przykładzie zbiór danych miałby następującą strukturę: 14, 19, 20, 24, 24, 25, 28.
- Sortowanie elementów w zbiorze danych pomoże również wykonać inne obliczenia, takie jak znalezienie trybu, średniej lub mediany zbioru danych.
Krok 2. Zidentyfikuj największe i najmniejsze liczby w zestawie danych
W tym zadaniu najmniejsza liczba w zbiorze danych to 14, a największa to 28.
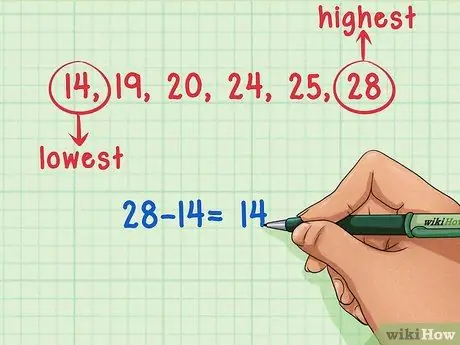
Krok 3. Odejmij najmniejszą liczbę w zestawie danych od największej liczby
Teraz, gdy już zidentyfikowałeś najmniejszą i największą liczbę w zestawie danych, wszystko, co musisz zrobić, to odjąć je od siebie. Odejmij 14 od 25 (25 – 14), aby otrzymać 11, zakres zbioru danych.
Krok 4. Wyraźnie oznacz zakres
Po znalezieniu zakresu oznacz go wyraźnie. Pomoże to uniknąć pomyłek z innymi obliczeniami statystycznymi, które być może będziesz musiał wykonać, takimi jak znajdowanie mediany, trybu lub średniej.
Porady
- Możesz również interpretować zakres w terminach algebraicznych, ale najpierw musisz zrozumieć pojęcie funkcji algebraicznej lub zestawu operacji na znanych liczbach. Ponieważ operacje funkcyjne mogą być wykonywane na dowolnej liczbie, nawet nieznanej, liczba ta jest oznaczona zmienną literową, zwykle x. Domena to zbiór możliwych wartości wejściowych, które można zastąpić nieznaną liczbą. Zatem zakres jest zbiorem możliwych wyników obliczeń, które otrzymujesz po wpisaniu jednej z wartości domeny i wykonaniu wszystkich operacji zdefiniowanych przez funkcję. Niestety nie ma możliwości obliczenia zakresu funkcji. Czasami wykres funkcji lub obliczanie wielu wartości może pokazać wyraźny wzór. Możesz także wykorzystać swoją wiedzę na temat domeny funkcji, aby odrzucić możliwe wartości wyjściowe (wyniki obliczeń) lub zawęzić zestaw danych reprezentujący zakres.
- Mediana dowolnego zbioru danych statystycznych reprezentuje medianę wartości zbioru danych pod względem rozkładu danych, a nie zakresu. Tak więc, chociaż możesz chcieć założyć, że mediana danego zestawu danych jest przedziałem podzielonym przez 2 – lub połowę przedziału – zwykle nie jest to prawdą. Aby znaleźć prawidłową medianę, musisz posortować elementy danych, a następnie poszukać elementu na środku listy. Ten element jest medianą. Na przykład, jeśli masz listę 29 elementów, 15. element ma ten sam zakres od początku listy i końca listy, więc 15. element jest medianą, niezależnie od tego, jak odnosi się wartość tego elementu Zakres.
