- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:15.
- Ostatnio zmodyfikowany 2025-01-23 12:43.
Każdy może uczyć się matematyki, niezależnie od tego, czy jest już na wyższym poziomie w szkole, czy po prostu chce ponownie doskonalić podstawy. Po omówieniu, jak być dobrym uczniem matematyki, ten artykuł nauczy Cię podstawowych postępów matematycznych i przedstawi podstawowe elementy, których będziesz musiał się nauczyć podczas każdej praktyki. Następnie w tym artykule zostaną omówione podstawy nauki arytmetyki, które pomogą zarówno dzieciom ze szkół podstawowych, jak i wszystkim, którzy chcą poznać podstawy tej dziedziny nauki.
Krok
Część 1 z 6: Jak zostać dobrym uczniem matematyki

Krok 1. Pojawiaj się w klasie
Kiedy opuszczasz zajęcia, powinieneś uczyć się pojęć od kolegów z klasy lub z podręcznika. Nigdy nie otrzymasz od znajomego streszczenia tekstowego tak bardzo, jak od nauczyciela.
- Przyjdź do klasy na czas. Zamiast tego przyjdź trochę wcześnie i otwórz zeszyt we właściwym miejscu, otwórz podręcznik i wyjmij kalkulator, aby być gotowym do rozpoczęcia, gdy nauczyciel będzie gotowy do nauczania.
- Wagarujesz tylko wtedy, gdy jesteś chory. Jeśli naprawdę tęsknisz za zajęciami, poproś kolegów z klasy, aby dowiedzieli się, o czym mówił nauczyciel i jaką pracę domową zadano.

Krok 2. Pracuj z nauczycielem
Jeśli twój nauczyciel pracuje nad problemem przed klasą, pracuj z nauczycielem, pracując nad problemem w zeszycie.
- Upewnij się, że Twoje notatki są jasne i łatwe do odczytania. Nie pisz tylko pytań. Zapisz również wszystko, co powie nauczyciel, co może poprawić twoje zrozumienie wyjaśnianych pojęć.
- Wypełnij przykładowe pytania zadane przez nauczyciela. Gdy nauczyciel chodzi po klasie podczas pracy, odpowiadaj na zadawane pytania.
- Weź udział, gdy nauczyciel rozwiąże problem. Nie czekaj, aż nauczyciel do ciebie zadzwoni. Zaproponuj odpowiedź, gdy znasz odpowiedź, i podnieś rękę, aby zadać pytanie, jeśli nie jesteś pewien materiału, którego się uczysz.

Krok 3. Odrób pracę domową tego samego dnia, w którym została oddana praca domowa
Jeśli odrabiasz pracę domową tego samego dnia, koncepcja jest wciąż świeża w twoim umyśle. Czasami odrabianie pracy domowej tego samego dnia nie jest możliwe. Upewnij się, że twoja praca domowa jest odrobiona, zanim pójdziesz na zajęcia.

Krok 4. Pracuj poza klasą, jeśli potrzebujesz pomocy
Odwiedzaj swojego nauczyciela podczas przerw lub w godzinach pracy.
- Jeśli masz centrum matematyczne w swojej szkole, sprawdź godziny otwarcia i poproś o pomoc.
- Dołącz do grupy badawczej. Dobra grupa badawcza składa się na ogół z 4 lub 5 osób o różnym poziomie umiejętności. Jeśli jesteś uczniem "C" w matematyce, dołącz do grupy 2 lub 3 uczniów z ocenami "A" lub "B", aby poprawić swoje umiejętności. Unikaj dołączania do grupy uczniów, których oceny są niższe niż twoje.
Część 2 z 6: Nauka matematyki w szkole

Krok 1. Zacznij od arytmetyki
W większości szkół uczniowie uczą się arytmetyki w szkole podstawowej. Arytmetyka obejmuje podstawy dodawania, odejmowania, mnożenia i dzielenia.
- Ćwicz pytania. Ciągłe wykonywanie zadań arytmetycznych to najlepszy sposób na prawidłowe zapamiętanie podstaw. Poszukaj oprogramowania, które umożliwi Ci pracę z wieloma różnymi zadaniami matematycznymi. Poszukaj również problemów z ramami czasowymi, aby poprawić swoją prędkość.
- Możesz także wyszukiwać problemy arytmetyczne online i pobierać aplikacje arytmetyczne na urządzenie mobilne.

Krok 2. Kontynuuj wstępną algebrę
To ćwiczenie dostarczy Ci podstawowych elementów, które będą Ci potrzebne do późniejszego rozwiązywania problemów z algebry.
- Dowiedz się więcej o ułamkach zwykłych i dziesiętnych. Nauczysz się dodawać, odejmować, mnożyć i dzielić ułamki zwykłe i dziesiętne. Jeśli chodzi o ułamki, dowiesz się, jak odejmować ułamki i tłumaczyć liczby połączone. Jeśli chodzi o ułamki dziesiętne, zrozumiesz wartości miejsc i będziesz mógł używać ułamków dziesiętnych w zadaniach fabularnych.
- Dowiedz się o proporcjach, proporcjach i procentach. Te pojęcia pomogą ci nauczyć się dokonywać porównań.
- Zapoznaj się z podstawową geometrią. Poznasz kształty i koncepcje 3D. Nauczysz się również pojęć, takich jak powierzchnia, obwód, objętość i powierzchnia, a także informacji o równoległych i prostopadłych liniach i kątach.
- Zapoznaj się z podstawowymi statystykami. We wstępie do algebry wprowadzenie do statystyki obejmuje zazwyczaj elementy wizualne, takie jak wykresy, wykresy punktowe, wykresy stemplowe i histogramy.
- Poznaj podstawy algebry. Obejmuje to takie pojęcia, jak rozwiązywanie prostych równań zawierających zmienne, poznawanie właściwości, takich jak właściwość rozdzielności, rysowanie prostych równań i rozwiązywanie nierówności.
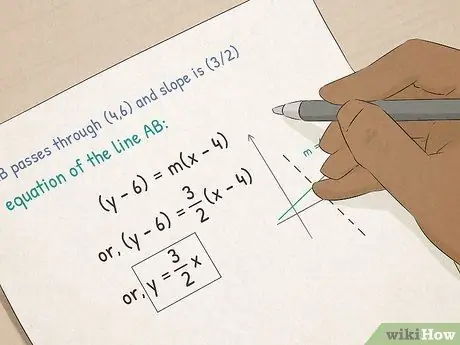
Krok 3. Przejdź do Algebry I
Na pierwszym roku algebry poznasz podstawowe symbole zawarte w algebrze. Nauczysz się również:
- Rozwiąż równania i nierówności zawierające zmienne. Dowiesz się, jak rozwiązywać te problemy na papierze i jak je rozwiązywać za pomocą zdjęć.
- Rozwiąż problemy fabularne. Zdziwisz się, jak wiele codziennych problemów napotkasz w przyszłości, które wymagają umiejętności rozwiązywania algebraicznych problemów fabularnych. Na przykład użyjesz algebry, aby dowiedzieć się, jaką stopę procentową zarabiasz na swoim koncie bankowym lub inwestycji. Możesz także użyć algebry, aby obliczyć, jak długo powinieneś podróżować na podstawie prędkości samochodu.
- Praca z wykładnikami. Kiedy zaczniesz rozwiązywać równania wielomianowe (wyrażenia, które zawierają liczby i zmienne), zrozumiesz, jak używać wykładników. Prawdopodobnie będą to ćwiczenia z notacją naukową. Kiedy już opanujesz wykładniki, możesz nauczyć się dodawać, odejmować, mnożyć i dzielić wyrażenia wielomianowe.
- Rozwiąż zadania z pierwiastkami kwadratowymi i kwadratowymi. Gdy opanujesz ten temat, będziesz w stanie zapamiętać kwadraty wielu liczb. Będziesz także mógł pracować z równaniami, które mają pierwiastki kwadratowe.
- Rozumieć funkcje i wykresy. W algebrze poznasz równania graficzne. Dowiesz się, jak obliczyć nachylenie linii, jak umieścić równanie w formie punkt-nachylenie i jak obliczyć wycinek x-i-y linii za pomocą formy przecięcia nachylenia.
- Poznaj układ równań. Czasami otrzymujesz 2 różne równania ze zmiennymi x i y i musisz rozwiązać x lub y dla obu równań. Na szczęście nauczysz się wielu sztuczek do rozwiązywania tych równań, w tym tworzenia wykresów, podstawienia i dodawania.

Krok 4. Przestudiuj geometrię
W geometrii poznasz właściwości linii, odcinków, kątów i kształtów.
- Nauczysz się na pamięć szeregu twierdzeń i wniosków, które pomogą Ci zrozumieć zasady geometrii.
- Dowiesz się, jak obliczyć powierzchnię koła, jak korzystać z twierdzenia Pitagorasa i jak znaleźć związek między kątami i bokami specjalnego trójkąta.
- W przyszłych standardowych testach, takich jak SAT, ACT i GRE, zobaczysz wiele pytań dotyczących geometrii.
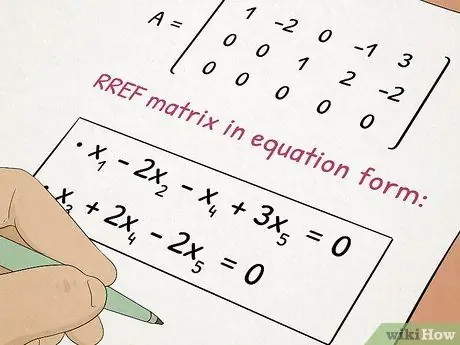
Krok 5. Weź udział w zajęciach z Algebry II
Algebra II opiera się na pojęciach, których nauczyłeś się w Algebrze I, dodając do złożonych tematów, takich jak równania kwadratowe i macierze.
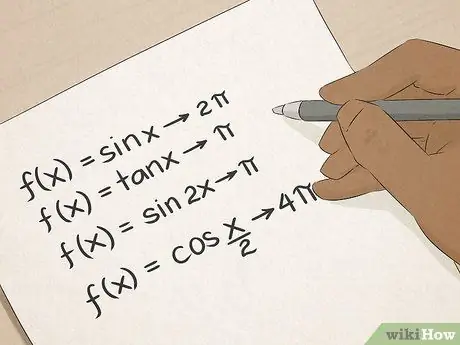
Krok 6. Mistrz trygonometrii
Znasz terminy trygonometryczne: sinus, cosinus, tangens i tak dalej. Trygonometria nauczy Cię wielu praktycznych sposobów obliczania kątów i długości linii, a te umiejętności będą bezcenne dla osób pracujących w budownictwie, architekturze, inżynierii lub geodezji.
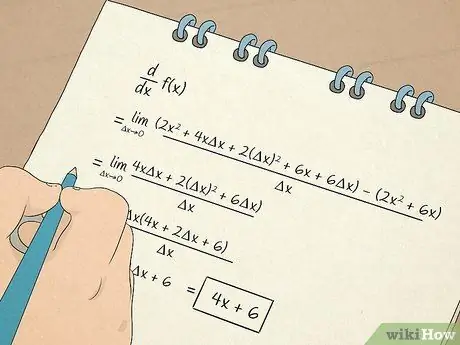
Krok 7. Wykonaj obliczenia matematyczne
Rachunek może brzmieć onieśmielająco, ale jest wspaniałym narzędziem do zrozumienia zachowania liczb lub otaczającego nas świata.
- Rachunek nauczy Cię funkcji i granic. Zobaczysz zachowanie liczb użytecznych funkcji, w tym funkcji e^x i logarytmicznych.
- Dowiesz się również, jak obliczać i pracować z instrumentami pochodnymi. Pierwsza pochodna dostarcza informacji na podstawie nachylenia linii stycznej do równania. Na przykład pochodna informuje o tempie, w jakim coś się zmienia w sytuacji nieliniowej. Druga pochodna powie ci, czy funkcja rośnie, czy maleje w określonym przedziale, dzięki czemu możesz określić wklęsłość funkcji.
- Całki nauczą Cię, jak obliczyć powierzchnię pod krzywą oraz jej objętość.
- Rachunek w liceum na ogół kończy się sekwencjami i sekwencjami. Chociaż uczniowie nie zobaczą wielu zastosowań obwodów, obwody są ważne dla osób studiujących równania różniczkowe.
Część 3 z 6: Podstawy matematyki - dodawanie mistrzów

Krok 1. Zacznij od faktów „+1”
Dodanie 1 do liczby prowadzi do najwyższej liczby na osi liczbowej. Na przykład 2 + 1 = 3.
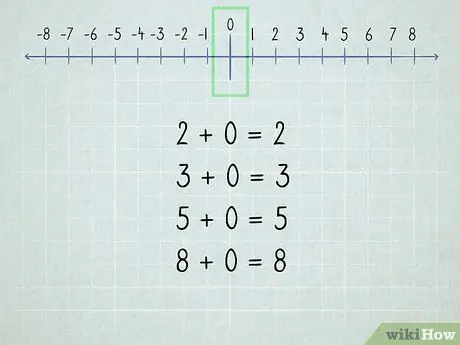
Krok 2. Zrozum zero
Wszystkie liczby dodawane do zera są tą samą liczbą, ponieważ „zero” oznacza „brak”.

Krok 3. Naucz się podwójnych liczb
Wiele liczb to problem, który polega na dodaniu dwóch równych liczb. Na przykład 3 + 3 = 6 jest przykładem równania obejmującego wiele liczb.

Krok 4. Użyj mapowania, aby dowiedzieć się o innych rozwiązaniach dodawania
W poniższym przykładzie dowiesz się, co się stanie, gdy dodasz 3 do 5, 2 i 1. Spróbuj samodzielnie rozwiązać problem „dodaj przez 2”.

Krok 5. Kontynuuj, aż liczba będzie większa niż 10
Naucz się dodawać 3 liczby razem, aby uzyskać liczbę większą niż 10.
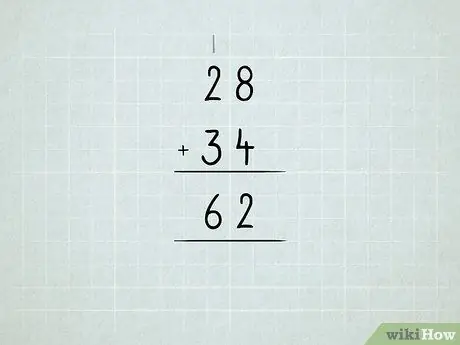
Krok 6. Dodaj większe liczby
Dowiedz się, jak przegrupowywać jednostki na dziesiątki, dziesiątki na setki i tak dalej.
- Najpierw zsumuj liczby w prawej kolumnie. 8 + 4 = 12, co oznacza, że masz 1 cyfrę 10 i 2 cyfrę 1. Wpisz cyfrę 2 pod kolumną jednostek.
-
Wpisz cyfrę 1 w kolumnie dziesiątek.
-
Zsumuj całą kolumnę dziesiątek.
Część 4 z 6: Podstawy matematyczne - strategie redukcji

Krok 1. Zacznij od „wstecz 1 cyfra
Odjęcie 1 od liczby powoduje powrót o 1 liczbę. Na przykład 4 - 1 = 3.

Krok 2. Naucz się odejmować liczby podwójne
Na przykład dodajesz liczby 5 + 5, aby uzyskać 10. Po prostu napisz równanie od tyłu, aby uzyskać 10 - 5 = 5.
- Jeśli 5 + 5 = 10, to 10 - 5 = 5.
-
Jeśli 2 + 2 = 4, to 4 - 2 = 2.

Krok 3. Zapamiętaj rodzinę faktów
Jako przykład:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Krok 4. Znajdź brakujące numery
Na przykład _ + 1 = 6 (odpowiedź to 5).

Krok 5. Zapamiętaj fakt odejmowania do 20

Krok 6. Przećwicz odejmowanie liczb jednocyfrowych od liczb dwucyfrowych bez pożyczania
Odejmij liczby w kolumnie jedności i zmniejsz liczby w kolumnie dziesiątek.
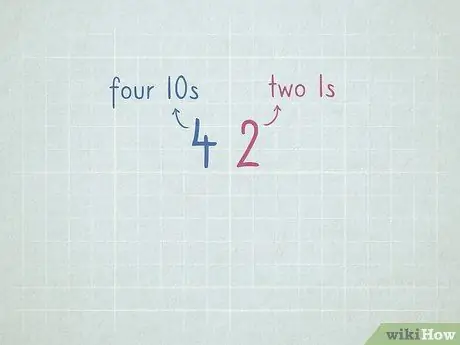
Krok 7. Przećwicz wartość miejsca, aby przygotować się do odejmowania przez pożyczanie
- 32 = 3 cyfry 10 i 2 cyfry 1.
- 64 = 6 cyfr 10 i 4 cyfry 1.
- 96 = _ numer 10 i _ numer 1.
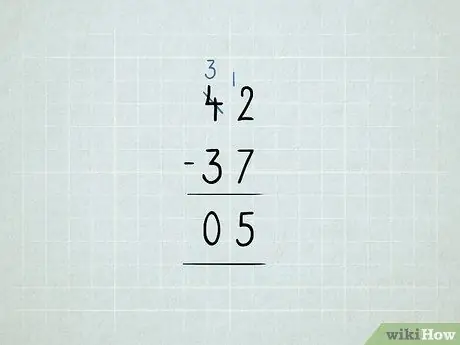
Krok 8. Odejmij pożyczając
- Chcesz odjąć 42 - 37. Zaczynasz od odjęcia 2 - 7 w kolumnie jednostek. Okazuje się, że to nie zadziałało!
-
Wypożycz liczbę 10 z kolumny dziesiątek i umieść ją w kolumnie jedności. Teraz masz 3 10 zamiast 4 10. Teraz masz 12 jedynek zamiast 2 jedynek.
-
Odejmij najpierw kolumnę jednostek: 12 - 7 = 5. Następnie sprawdź kolumnę dziesiątek. Ponieważ 3 - 3 = 0, nie musisz zapisywać cyfry 0. Twoja odpowiedź to 5.
Część 5 z 6: Podstawy matematyki - mnożenie wzorca

Krok 1. Zacznij od cyfry 1 i cyfry 0
Wszystkie liczby pomnożone przez 1 są takie same jak sama liczba. Każda liczba pomnożona przez 0 jest równa zeru.

Krok 2. Zapamiętaj tabliczkę mnożenia

Krok 3. Ćwicz z zadaniami z mnożenia pojedynczych cyfr

Krok 4. Pomnóż liczbę 2-cyfrową przez liczbę 1-cyfrową
- Pomnóż prawą dolną liczbę przez prawą górną liczbę.
-
Pomnóż prawą dolną liczbę przez lewą górną liczbę.
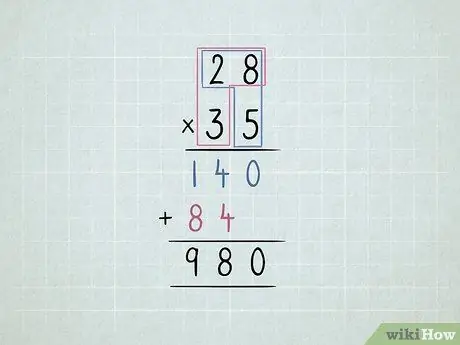
Krok 5. Pomnóż 2 2-cyfrowe liczby
- Pomnóż prawą dolną liczbę przez prawą górną liczbę, a następnie przez lewą górną liczbę.
-
Przesuń drugi rząd o jedną cyfrę w lewo.
- Pomnóż lewą dolną liczbę przez prawą górną liczbę, a następnie lewą górną liczbę.
-
Dodaj wszystkie kolumny.
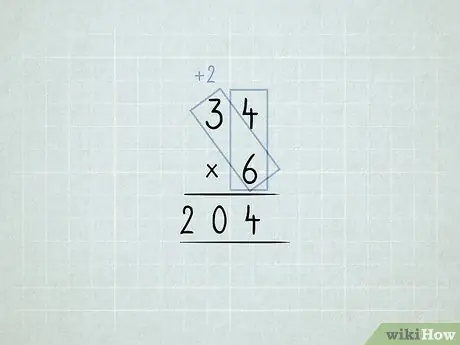
Krok 6. Pomnóż i przegrupuj kolumny
- Chcesz pomnożyć 34 x 6. Zaczynasz od pomnożenia kolumny jednostek (4 x 6), ale nie możesz mieć 24 jedynek w kolumnie jedności.
-
Przechowuj 4 jedynki w kolumnie jednostek. Przenieś 2 10s do kolumny dziesiątek.
-
Pomnóż 6 x 3, co daje 18. Dodaj 2, które przeniosłeś, co daje 20.
Część 6 z 6: Podstawy matematyczne - odkrywanie problemów z podziałem

Krok 1. Pomyśl o dzieleniu w przeciwieństwie do mnożenia
#* Jeśli 4 x 4 = 16, to 16 / 4 = 4.
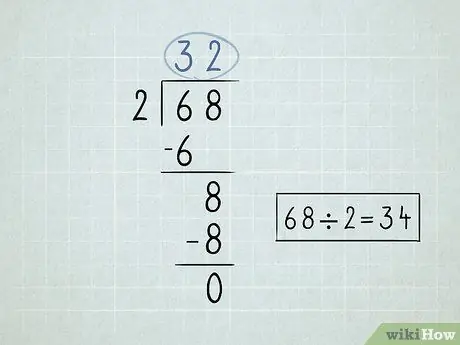
Krok 2. Zapisz swój problem z dzieleniem
- Podziel liczbę po lewej stronie symbolu dzielenia lub dzielnika przez pierwszą liczbę poniżej symbolu dzielnika. Ponieważ 6 / 2 = 3, wpiszesz liczbę 3 nad symbolem dzielenia.
-
Pomnóż liczbę powyżej symbolu dzielenia przez dzielnik. Przenieś wynik na dół pierwszej liczby pod symbolem podziału. Ponieważ 3 x 2 = 6, obniżysz liczbę 6 w dół.
- Odejmij 2 liczby, które zapisałeś. 6 - 6 = 0. Możesz zostawić 0 puste, ponieważ zazwyczaj nie zaczynasz liczb od 0.
-
Podaj drugą liczbę, która znajduje się poniżej symbolu podziału.
- Podziel liczbę, którą obniżasz, przez dzielnik. W tym przypadku 8 / 2 = 4. Wpisz cyfrę 4 nad symbolem podziału.
-
Pomnóż prawą górną liczbę przez dzielnik i sprowadź liczbę w dół. 4 x 2 = 8.
-
Odejmij te liczby. Ostateczne odejmowanie zwraca zero, co oznacza, że rozwiązałeś problem. 68 x 2 = 34.

Krok 3. Oblicz także resztę
Niektóre z dzielników nie są w pełni podzielone na inne liczby. Jeśli zakończyłeś ostatnie odejmowanie i nie masz więcej liczb do obliczenia, to ostatnia liczba jest resztą.






