- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:32.
- Ostatnio zmodyfikowany 2025-06-01 06:07.
System liczb dziesiętnych (dziesiętny) ma dziesięć możliwych wartości (0, 1, 2, 3, 4, 5, 6, 7, 8 lub 9) dla każdej pozycji liczbowej. W przeciwieństwie do tego, binarny (podstawowy) system liczbowy ma tylko dwie możliwe wartości reprezentowane przez 0 i 1 dla każdej pozycji liczbowej. Ponieważ system liczb binarnych jest językiem wewnętrznym komputerów elektronicznych, poważni programiści wiedzą, jak dokonać konwersji z systemu liczb dziesiętnych na system liczb dwójkowych. Wykonaj te proste kroki, a także jak opanować tę konwersję.
Krok
Metoda 1 z 2: Krótkie dzielenie przez dwa z resztą

Krok 1. Określ problem
W tym przykładzie przekonwertujmy liczbę dziesiętną 15610 być liczbą binarną. Wpisz liczbę dziesiętną jako liczbę do podzielenia w symbolu dzielenia odwróconego. Napisz podstawę docelowego systemu liczbowego (w tym przykładzie „2” dla binarnego) jako dzielnik poza krzywą symbolu dzielenia.
- Ta metoda jest znacznie łatwiejsza do zrozumienia na papierze i znacznie łatwiejsza dla początkujących, ponieważ dzieli się tylko przez dwa.
- Aby uniknąć nieporozumień przed i po konwersji, zapisz numer podstawowy systemu liczbowego, który obliczasz, jako indeks dolny (małe litery pisane pod normalnymi literami jako znak odróżniający) dla każdej liczby. W tym przykładzie liczba dziesiętna będzie miała indeks 10, a liczba binarna będzie miała indeks 2.

Krok 2. Dokonaj podziału
Wpisz odpowiedź całkowitą (iloraz) pod symbolem długiego dzielenia, a resztę (0 lub 1) na prawo od dzielonej liczby.
Ponieważ dzielimy przez dwa, gdy dzielona liczba jest parzysta, wtedy reszta wynosi 0, a gdy dzielona liczba jest nieparzysta, reszta wynosi 1

Krok 3. Kontynuuj dzielenie, aż osiągnie zero
Kontynuuj w dół, dzieląc każdy nowy iloraz przez dwa i zapisując resztę po prawej stronie każdej podzielonej liczby. Zatrzymaj się, gdy iloraz wynosi zero.

Krok 4. Zapisz nową liczbę binarną
Zaczynając od najniższej pozostałej liczby, odczytaj kolejność reszty w kolejności rosnącej do góry. W tym przykładzie powinieneś otrzymać wynik 10011100. Jest to binarny odpowiednik liczby dziesiętnej 156. Lub, jeśli napisano z jej bazowym indeksem liczbowym: 15610 = 100111002.
Metodę tę można zmodyfikować, aby konwertować z podstawy dziesiętnej na dowolną podstawę liczbową. Dzielnikiem jest 2, ponieważ podstawą systemu liczb docelowych jest podstawa 2 (dwójkowa). Jeśli podstawą docelowego systemu liczbowego jest inna podstawa, zastąp liczbę o podstawie 2 w tej metodzie odpowiednią liczbą o podstawie. Na przykład, jeśli docelową podstawą jest liczba o podstawie 9, zamień liczbę o podstawie 2 na 9. Ostateczny wynik będzie bezpośrednio w postaci docelowej liczby o podstawie
Metoda 2 z 2: Wyprowadzanie potęgi dwójki i odejmowanie

Krok 1. Zacznij od stworzenia tabeli
Zapisz potęgi dwóch liczb podstawowych w „podstawie tabeli 2” od prawej do lewej. Zacznij od 20, napisz jako „1”. Podnieś rangę o 1 za każdą rangę. Uzupełnij tabelę, aż uzyskasz liczbę, która jest najbardziej zbliżona do liczby w systemie liczb dziesiętnych, który obliczasz. W tym przykładzie przekonwertujmy liczbę dziesiętną 15610 być liczbą binarną.

Krok 2. Znajdź liczbę o największej potędze podstawy 2
Wybierz z tabeli największą liczbę, która jest równa lub mniejsza od liczby do przeliczenia. Liczba 128 jest liczbą o największej potędze podstawy 2 i jest również mniejsza od 156, więc wpisz liczbę "1" pod tym polem w tabeli, gdzie największa liczba z tabeli znajduje się po lewej stronie (patrz tabela na obrazku powyżej). Następnie odejmij 128 od liczby początkowej, otrzymasz: 156 - 128 = 28.
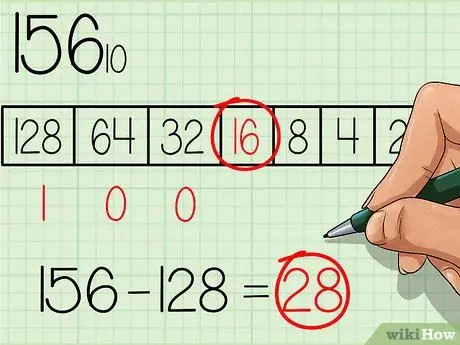
Krok 3. Przejdź do następnej mniejszej mocy w tabeli
Używając nowej liczby (28), przejdź przez tabelę od lewej do prawej, sprawdzając, czy liczby są równe lub mniejsze od nowej liczby. Liczba 64 jest nie mniejsza niż 28, więc wpisz liczbę „0” pod polem 64. Kontynuuj, aż znajdziesz liczbę równą lub mniejszą niż 28.
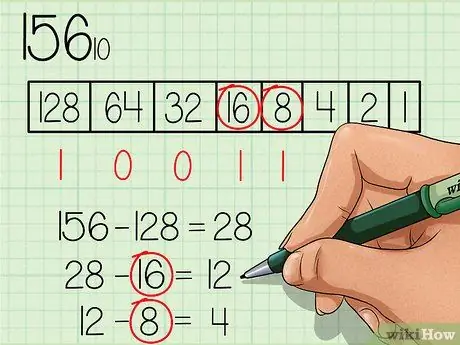
Krok 4. Odejmij każdą liczbę, która jest równa lub mniejsza od nowej liczby w sposób ciągły i zaznacz liczbę „1” poniżej pola dla odpowiedniej liczby
Liczba 16 jest mniejsza niż 28, więc wpisz liczbę „1” pod polem 16 i odejmij 16 od 28, aby uzyskać nową liczbę 12. Liczba 8 jest mniejsza niż 12, więc wpisz liczbę „1” pod pole liczby 8 i odejmij 8 od 12, aby uzyskać nową liczbę 4.

Krok 5. Kontynuuj, aż dojdziesz do końca stołu
Pamiętaj, aby zaznaczyć „1” pod każdym polem dla liczb, które są równe lub mniejsze niż nowa liczba, oraz „0” pod każdym polem dla liczb, które są nadal większe niż nowa liczba.
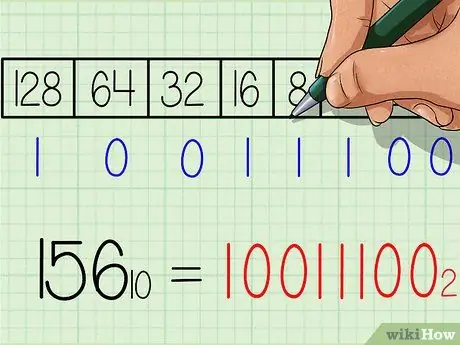
Krok 6. Zapisz odpowiedź na liczbę binarną
Numer będzie dokładnie taki sam od lewej do prawej, jak rząd liczb „1” i „0” na dole tabeli. Powinieneś otrzymać wynik 10011100. Jest to binarny odpowiednik liczby dziesiętnej 156. Lub przy zapisie z indeksem dolnym: 15610 = 100111002.
Powtórzenie tej metody może pomóc Ci zapamiętać potęgi podstawy dwa, więc możesz pominąć krok 1
Porady
- Program Kalkulator wbudowany w system operacyjny może wykonać tę konwersję za Ciebie, ale jako programista najlepiej zacząć od dobrego zrozumienia działania konwersji. Opcje konwersji w programie Kalkulator można wyświetlić, otwierając menu „Widok” i wybierając „Programator” (dla Windows 7 i 8).
- Konwersja w przeciwnym kierunku, tj. z systemu liczb binarnych na dziesiętne, jest zwykle łatwiejsza do nauczenia.
- Często ćwicz konwersję liczb dziesiętnych na binarne, aby stać się bardziej ekspertem.






